题目内容
已知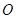 为坐标原点,
为坐标原点,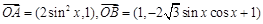 ,
,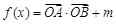 .
.
(Ⅰ)若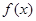 的定义域为
的定义域为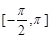 ,求
,求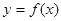 的单调递增区间;
的单调递增区间;
(Ⅱ)若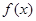 的定义域为
的定义域为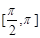 ,值域为
,值域为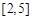 ,求
,求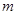 的值.
的值.
【答案】
(Ⅰ)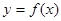 的增区间为:
的增区间为: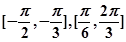 ;(Ⅱ)
;(Ⅱ)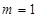 .
.
【解析】
试题分析:(Ⅰ)由向量的数量积的坐标运算得: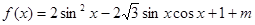 ,然后降次化一得
,然后降次化一得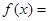
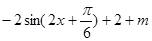 .首先由
.首先由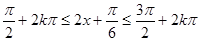
 得
得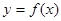 在
在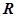 上的单调递增区间为
上的单调递增区间为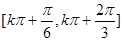
 .又因为
.又因为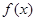 的定义域为
的定义域为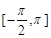 ,所以取
,所以取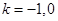 ,便得
,便得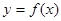 在
在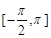 上的单调递增区间.
上的单调递增区间.
(Ⅱ)当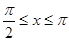 时,
时,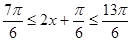 .结合正弦函数的图象可得,
.结合正弦函数的图象可得,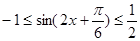
从而得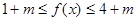 再结合已知条件得:
再结合已知条件得: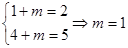 .
.
试题解析:(Ⅰ)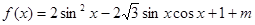
=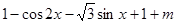 =
=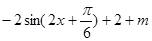 3分
3分
由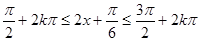

得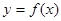 在
在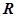 上的单调递增区间为
上的单调递增区间为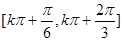

又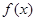 的定义域为
的定义域为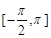 ,
,
∴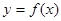 的增区间为:
的增区间为: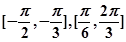 (中间若用“
(中间若用“ ”扣2分) 7分
”扣2分) 7分
(Ⅱ)当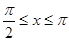 时,
时,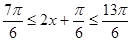 ∴
∴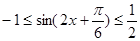
∴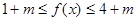 ,∴
,∴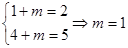 12分
12分
考点:1、向量的数量积;2、三角恒等变换;3、三角函数的单调性及范围.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案
相关题目






 为坐标原点,向量
为坐标原点,向量 ,
,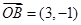 ,且
,且 ,则点
,则点 的坐标为
的坐标为 B.
B.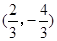 C.
C. D.
D.
 为坐标原点,点
为坐标原点,点 ,点
,点 满足条件
满足条件 ,则
,则 的最大值为_____________。
的最大值为_____________。 为坐标原点,且
为坐标原点,且 ,则
,则 点的坐标为 .
点的坐标为 . 为坐标原点,
为坐标原点, ,
, 。
。 的单调递增区间;
的单调递增区间; 的定义域为
的定义域为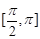 ,值域为
,值域为 ,求
,求 的值。
的值。