题目内容
已知关于![]() 的不等式
的不等式![]() ,其中
,其中![]() 。
。
⑴试求不等式的解集![]() ;
;
⑵对于不等式的解集![]() ,若满足
,若满足![]() (其中
(其中![]() 为整数集)。试探究集合
为整数集)。试探究集合![]() 能否为有限集?若能,求出使得集合
能否为有限集?若能,求出使得集合![]() 中元素个数最少的
中元素个数最少的![]() 的所有取值,并用列举法表示集合
的所有取值,并用列举法表示集合![]() ;若不能,请说明理由。
;若不能,请说明理由。
(1)见解析(2)![]() ,故集合
,故集合![]()
解析:
(1)当![]() 时,
时,![]() ;当
;当![]() 且
且![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ;(不单独分析
;(不单独分析![]() 时的情况不扣分)
时的情况不扣分)
当![]() 时,
时,![]() 。(10分)
。(10分)
(2)由(1)知:当![]() 时,集合
时,集合![]() 中的元素的个数无限;
中的元素的个数无限;
当![]() 时,集合
时,集合![]() 中的元素的个数有限,此时集合
中的元素的个数有限,此时集合![]() 为有限集。(12分)
为有限集。(12分)
因为![]() ,当且仅当
,当且仅当![]() 时取等号,
时取等号,
所以当![]() 时,集合
时,集合![]() 的元素个数最少。(14分)
的元素个数最少。(14分)
此时![]() ,故集合
,故集合![]() 。(16分)
。(16分)

练习册系列答案
相关题目
 是公差为
是公差为 的等差数列,其前
的等差数列,其前 项和为
项和为 .
. ,
, ,
,
 时,
时,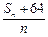 的最小值;
的最小值; ;
; ,使得对任意正整数
,使得对任意正整数 的不等式
的不等式 的最小正整数解为
的最小正整数解为 ?若存在,则求
?若存在,则求 是公差为
是公差为 的等差数列,其前
的等差数列,其前 项和为
项和为 .
. ,
, ,
,
 时,
时, 的最小值;
的最小值; ;
; ,使得对任意正整数
,使得对任意正整数 的不等式
的不等式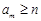 的最小正整数解为
的最小正整数解为 ?若存在,则求
?若存在,则求 是公差为
是公差为 的等差数列,其前
的等差数列,其前 项和为
项和为 .
. ,
, ,
,
 时,
时, 的最小值;
的最小值; ;
; ,使得对任意正整数
,使得对任意正整数 的不等式
的不等式 的最小正整数解为
的最小正整数解为 ?若存在,则求
?若存在,则求