题目内容
12.已知函数f(x)=xlnx.(Ⅰ)求f(x)的单调区间及最小值;
(Ⅱ)f(x)≥$\frac{ax-1}{2}$在(0,+∞)上恒成立,试求实数a的取值范围.
分析 (Ⅰ)由f(x)=xlnx,知f′(x)=1+lnx,x>0,由此能求出函数f(x)的单调区间和极小值、最小值;
(Ⅱ)由f(x)≥$\frac{ax-1}{2}$在(0,+∞)上恒成立,可得a≤2lnx+$\frac{1}{x}$在(0,+∞)上恒成立,令g(x)=2lnx+$\frac{1}{x}$,x>0,求出导数,求得最小值,由此能够求出实数a的取值范围.
解答 解:(Ⅰ)∵f(x)=xlnx,
∴f′(x)=1+lnx,x>0,
∵f′(x)>0解得x>$\frac{1}{e}$,f′(x)<0解得0<x<$\frac{1}{e}$,
∴函数f(x)的减区间为(0,$\frac{1}{e}$),增区间为($\frac{1}{e}$+∞),
f(x)在x=$\frac{1}{e}$取得极小值,也为最小值,且为-$\frac{1}{e}$.
(Ⅱ)∵f(x)≥$\frac{ax-1}{2}$在(0,+∞)上恒成立,
∴a≤2lnx+$\frac{1}{x}$在(0,+∞)上恒成立,
令g(x)=2lnx+$\frac{1}{x}$,x>0,g′(x)=$\frac{2}{x}$-$\frac{1}{{x}^{2}}$=$\frac{2x-1}{{x}^{2}}$,
当x>$\frac{1}{2}$时,g′(x)>0,g(x)是增函数,
当0<x<$\frac{1}{2}$时,g′(x)<0,g(x)是减函数,
g(x)在x=$\frac{1}{2}$处取得极小值,也为最小值,且为2-2ln2.
∴a≤g($\frac{1}{2}$)=2-2ln2.
即实数a的取值范围是(-∞,2-2ln2].
点评 本题考查利用导数求函数的单调区间和实数的取值范围的方法,解题时要认真审题,仔细解答,注意等价转化思想的合理运用.

 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案(1)若从这这4个品牌共5个批次的食用油中任选3个批次进行某项检测,求抽取的3个批次的食用油至少有一个是A品牌的概率.
(2)若对这4个品牌共5个批次的食用油进行综合检测,其检测结果如下(综合评估满分为10分):
| 品牌 | A1 | A2 | B | C | D |
| 得分 | 8 | 8 | 8.8 | 9.6 | 9.8 |

| A. | $\frac{1}{2}{a}^{2}$ | B. | $\frac{1}{4}$a2 | C. | $\frac{\sqrt{2}}{4}{a}^{2}$ | D. | $\frac{\sqrt{3}}{4}$a2 |
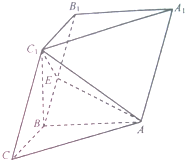 如图,在三棱柱ABC-1B1C1中,已知AB⊥侧面BB1CC1,BC=$\sqrt{2}$,AB=BB1=2,∠BCC1=$\frac{π}{4}$,点E为棱BB1的中点
如图,在三棱柱ABC-1B1C1中,已知AB⊥侧面BB1CC1,BC=$\sqrt{2}$,AB=BB1=2,∠BCC1=$\frac{π}{4}$,点E为棱BB1的中点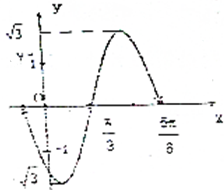 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的图象与x轴的两个交点坐标分别为($\frac{π}{3}$,0)和($\frac{5}{6}$π,0),其部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的图象与x轴的两个交点坐标分别为($\frac{π}{3}$,0)和($\frac{5}{6}$π,0),其部分图象如图所示.