题目内容
已知双曲线C: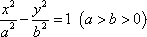 和圆O:x2+y2=b2(其中原点O为圆心),过双曲线C上一点P(x0,y0)引圆O的两条切线,切点分别为A、B.
和圆O:x2+y2=b2(其中原点O为圆心),过双曲线C上一点P(x0,y0)引圆O的两条切线,切点分别为A、B.
(1)若双曲线C上存在点P,使得∠APB=90°,求双曲线离心率e的取值范围;
(2)求直线AB的方程;
(3)求三角形OAB面积的最大值.
解析:
|
解:(1)因为 由 因为 故双曲线离心率 (2)方法1:因为 所以以点 因为圆 所以联立方程组 消去 方法2:设 则 因为 整理得 因为 因为 因为 所以直线 即 所以直线 方法3:设 则 因为 整理得 因为 这说明点 同理点 所以 (3)由(2)知,直线 所以点 因为 所以三角形 以下给出求三角形 方法1:因为点 所以 设 所以 因为 所以当 所以 当 当 综上可知,当 方法2:设 因为点 所以 令 所以当 所以 当 当 综上可知,当 方法3:设 因为点 所以 令 所以 因为 当 当 综上可知,当
|

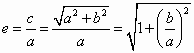
 . 4分
. 4分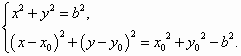 7分
7分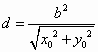 .
.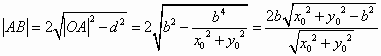 ,
,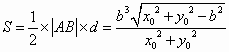 . 10分
. 10分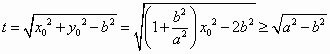 ,
,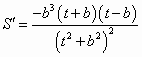 ,
,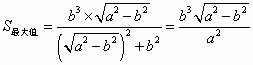 .
.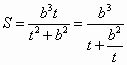 . 11分
. 11分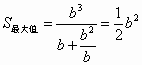 , 13分
, 13分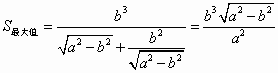 .
.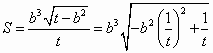 . 11分
. 11分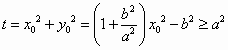 .
.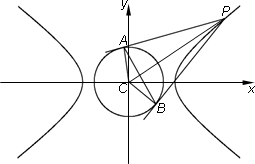
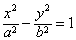 (a>b>0)和圆O:x2+y2=b2(其中原点O为圆心),过双曲线C上一点P(x0,y0)引圆O的两条切线,切点分别为A,B。
(a>b>0)和圆O:x2+y2=b2(其中原点O为圆心),过双曲线C上一点P(x0,y0)引圆O的两条切线,切点分别为A,B。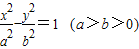 和圆O:x2+y2=b2(其中原点O为圆心),过双曲线C上一点P(x,y)引圆O的两条切线,切点分别为A、B.
和圆O:x2+y2=b2(其中原点O为圆心),过双曲线C上一点P(x,y)引圆O的两条切线,切点分别为A、B. 和圆O:x2+y2=b2(其中原点O为圆心),过双曲线C上一点P(x,y)引圆O的两条切线,切点分别为A、B.
和圆O:x2+y2=b2(其中原点O为圆心),过双曲线C上一点P(x,y)引圆O的两条切线,切点分别为A、B.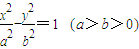 和圆O:x2+y2=b2(其中原点O为圆心),过双曲线C上一点P(x,y)引圆O的两条切线,切点分别为A、B.
和圆O:x2+y2=b2(其中原点O为圆心),过双曲线C上一点P(x,y)引圆O的两条切线,切点分别为A、B.