题目内容
8.已知集合A={x|3≤x<7},函数f(x)=lg(-x2+12x-20)的定义域为集合B,集合C={x|5-a<x<a}.(1)求B,A∪B,(∁RA)∩B;
(2)若C⊆(A∪B),求a的取值范围.
分析 (1)求出f(x)的定义域确定出B,即可求出A与B的并集,以及A补集与B的交集即可;
(2)根据C为A与B的并集,分C为空集与C不为空集两种情况,求出a的范围即可.
解答 解:(1)由函数f(x)=lg(-x2+12x-20),得到-x2+12x-20>0,
整理得:x2-12x+20<0,即(x-2)(x-10)<0,
解得:2<x<10,即B=(2,10),
∵A=[3,7),
∴A∪B=(2,10),∁RA=(-∞,3)∪[7,+∞),
则(∁RA)∩B=(2,3)∪[7,10);
(2)∵C⊆(A∪B),A∪B=(2,10),C=(5-a,a),
∴当C=∅时,5-a≥a,即a≤$\frac{5}{2}$,满足题意;
当C≠∅时,则有$\left\{\begin{array}{l}{5-a<a}\\{5-a≥2}\\{a≤10}\end{array}\right.$,
解得:$\frac{5}{2}$<a≤3,
综上,a的范围为a≤3.
点评 此题考查了交、并、补集的混合运算,熟练掌握各自的定义是解本题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
13.已知直线y=k(x-2)(k>0)与抛物线y2=8x相交于点A,B两点,F为抛物线的焦点,若|FA|=2|FB|,则k的值为( )
| A. | 4 | B. | 8 | C. | 2$\sqrt{2}$ | D. | 2$\sqrt{3}$ |
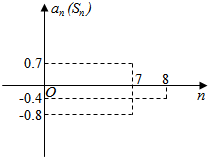 已知等差数列{an}的前n项和为Sn,在同一坐标系中,an=f(n)及Sn=g(n)的部分图象如图所示.
已知等差数列{an}的前n项和为Sn,在同一坐标系中,an=f(n)及Sn=g(n)的部分图象如图所示. 如图,空间四边形ABCD各边边长均为a,M,N分别是对角线BD,AC的中点.
如图,空间四边形ABCD各边边长均为a,M,N分别是对角线BD,AC的中点.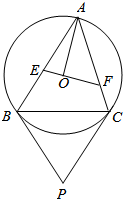 如图,锐角△ABC内接于圆0.过圆心0且垂直于半径0A的直线分别交边AB、AC于点E、F.设圆0在B、C两点处的切线相交于点P.求证:直线AP平分线段EF.
如图,锐角△ABC内接于圆0.过圆心0且垂直于半径0A的直线分别交边AB、AC于点E、F.设圆0在B、C两点处的切线相交于点P.求证:直线AP平分线段EF.