题目内容
四位同学在研究函数f(x)=-
（x∈R）时，分别给出下面四个结论：
①函数f（x）的值域为（-1，1）；
②若x1，x2∈R且x1＜x2＜0，则一定有
＞
；
③若x1，x2∈R且x1＜x2，则一定有
≥
；
④若集合M=[a，b]，N={y|y=f（x），x∈M}，则使M=N成立的有序实数对（a，b）只有一个．
则上述四个结论中正确的是（ ）
| x |
| 1+|x| |
①函数f（x）的值域为（-1，1）；
②若x1，x2∈R且x1＜x2＜0，则一定有
| f(x1) |
| x1 |
| f(x2) |
| x2 |
③若x1，x2∈R且x1＜x2，则一定有
| f(x1) |
| x1 |
| f(x2) |
| x2 |
④若集合M=[a，b]，N={y|y=f（x），x∈M}，则使M=N成立的有序实数对（a，b）只有一个．
则上述四个结论中正确的是（ ）
| A、①② | B、①③ | C、①④ | D、②④ |
分析：作出函数f(x)=-
（x∈R）的图象，依据图象判断①④．②③借助图象及其几何意义判断．
| x |
| 1+|x| |
解答：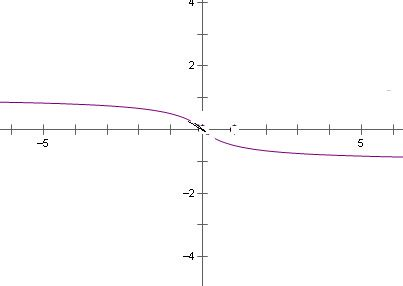
解：由图象知①正确，
对于②若x1，x2∈R且x1＜x2＜0，则一定有
＞
，表示（x1，f（x1））与（0，0）连线的斜率大于（x2，f（x2））与（0，0）连线的斜率，由图象知这一结论正确．
对于③，其结论与②相悖，故不正确
④这样的数对的个数超过一个，故不正确．
故应选A．
解：由图象知①正确，对于②若x1，x2∈R且x1＜x2＜0，则一定有
| f(x1) |
| x1 |
| f(x2) |
| x2 |
对于③，其结论与②相悖，故不正确
④这样的数对的个数超过一个，故不正确．
故应选A．
点评：考查函数的单调性每一点处切线的斜率的变化，函数本身的特征．本解法借助图象，以形助数，是解题的好方法．
练习册系列答案
相关题目
(x∈R)时，分别给出下面四个结论：
对任意n∈N*恒成立．你认为上述四个结论中正确的有________