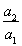题目内容
设Sn是公差不为0的等差数列{an}的前n项和,且S1,S2,S4成等比数列,则
等于( )
| a2 |
| a1 |
| A、1 | B、2 | C、3 | D、4 |
分析:由S1,S2,S4成等比数列,根据等比数列的性质得到S22=S1S4,然后利用等差数列的前n项和的公式分别表示出各项后,代入即可得到首项和公差的关系式,根据公差不为0,即可求出公差与首项的关系并解出公差d,然后把所求的式子利用等差数列的通项公式化简后,把公差d的关系式代入即可求出比值.
解答:解:由S1,S2,S4成等比数列,
∴(2a1+d)2=a1(4a1+6d).
∵d≠0,∴d=2a1.
∴
=
=
=3.
故选C
∴(2a1+d)2=a1(4a1+6d).
∵d≠0,∴d=2a1.
∴
| a2 |
| a1 |
| a1+d |
| a1 |
| 3a1 |
| a1 |
故选C
点评:此题考查学生掌握等比数列的性质,灵活运用等差数列的通项公式及前n项和的公式化简求值,是一道综合题.

练习册系列答案
 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目