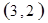题目内容
已知抛物线![]() 的焦点为
的焦点为![]() 是抛物线上横坐标为
是抛物线上横坐标为![]() ,且位于
,且位于![]() 轴上方的点,
轴上方的点,![]() 到抛物线准线的距离等于
到抛物线准线的距离等于![]() .过
.过![]() 作
作![]() 垂直于
垂直于![]() 轴,垂足为
轴,垂足为![]() ,
,![]() 的中点为
的中点为![]() .
.
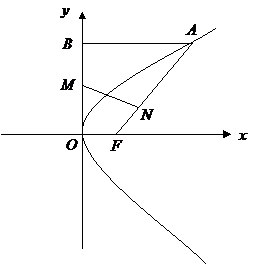 求抛物线方程;
求抛物线方程;
过![]() 作
作![]() ,垂足为
,垂足为![]() ,求点
,求点![]() 的坐标;
的坐标;
以![]() 为圆心,
为圆心,![]() 为半径作圆
为半径作圆![]() .当
.当![]() 是
是![]() 轴上一动点
轴上一动点
时,讨论直线![]() 与圆
与圆![]() 的位置关系.
的位置关系.
(1)抛物线方程为![]() . 2)
. 2)![]() .
.
当![]() 时,直线
时,直线![]() 与圆
与圆![]() 相离;当
相离;当![]() 时,直线
时,直线![]() 到圆
到圆![]() 相切;
相切;
当![]() 时,直线
时,直线![]() 与圆
与圆![]() 相交.
相交.
解析:
(1)抛物线![]() 的准线为
的准线为![]() ,于是,
,于是,![]() .
.
![]() ,
,![]() 抛物线方程为
抛物线方程为![]() .
.
(2)![]() 点
点![]() 的坐标是
的坐标是![]() .由题意得
.由题意得![]() .
.
又![]() ,
,![]() ;
;![]() ,
,![]() ,则
,则![]() 的方程为
的方程为![]() ,
,
![]() 的方程为
的方程为![]() ,解方程组
,解方程组 ,得
,得![]() ,
,![]() .
.
(3)由题意得,圆![]() 的圆心是点
的圆心是点![]() ,半径为
,半径为![]() .
.
当![]() 时,直线
时,直线![]() 的方程为
的方程为![]() ,此时,直线
,此时,直线![]() 与圆
与圆![]() 相离,
相离,
当![]() 时,直线
时,直线![]() 的方程为
的方程为![]() ,即为
,即为![]() ,
,
圆心![]() 到直线
到直线![]() 的距离
的距离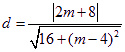 .
.
令![]() ,解得
,解得![]() .
.![]() 当
当![]() 时,直线
时,直线![]() 与圆
与圆![]() 相离;
相离;
当![]() 时,直线
时,直线![]() 到圆
到圆![]() 相切;当
相切;当![]() 时,直线
时,直线![]() 与圆
与圆![]() 相交.
相交.

练习册系列答案
相关题目
已知抛物线的焦点坐标是F(0,-2),则它的标准方程为( )
| A、x2=-8y | B、x2=3y | C、y2=-3x | D、y2=3x |
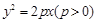 的焦点为
的焦点为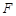 ,点
,点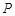 是抛物线上的一点,且其纵坐标为4,
是抛物线上的一点,且其纵坐标为4, .
.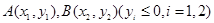 是抛物线上的两点,
是抛物线上的两点,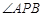 的角平分线与
的角平分线与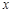 轴垂直,求
轴垂直,求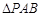 的面积最大时直线
的面积最大时直线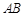 的方程.
的方程.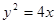 的焦点为F,A, B是该抛物线上的两点,弦AB过焦点F,且
的焦点为F,A, B是该抛物线上的两点,弦AB过焦点F,且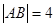 ,则线段AB的中点坐标是( )
,则线段AB的中点坐标是( )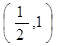 B.
B.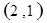 C.
C.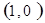 D.
D.