题目内容
有甲、乙两个班级进行数学考试,按照大于或等于85分为优秀,85分以下为非优秀统计成绩后,得到如下的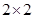 列联表:已知从全部210人中随机抽取1人为优秀的概率为
列联表:已知从全部210人中随机抽取1人为优秀的概率为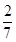 .
.
| | 优秀 | 非优秀 | 总计 |
| 甲班 | 20 | | |
| 乙班 | | 60 | |
| 合计 | | | 210 |
(Ⅰ)请完成上面的
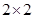 列联表,并判断若按99%的可靠性要求,能否认为“成绩与班级有关”;
列联表,并判断若按99%的可靠性要求,能否认为“成绩与班级有关”;(Ⅱ)从全部210人中有放回抽取3次,每次抽取1人,记被抽取的3人中的优秀人数为
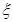 ,若每次抽取的结果是相互独立的,求
,若每次抽取的结果是相互独立的,求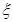 的分布列及数学期望
的分布列及数学期望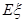 .
.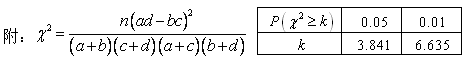
(Ⅰ) 优秀 非优秀 总计 甲班 20 90 110 乙班 40 60 100 合计 60 150 210 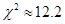 所以按照99%的可靠性要求,能够判断成绩与班级有关。
所以按照99%的可靠性要求,能够判断成绩与班级有关。
(Ⅱ)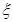 的分布列为
的分布列为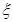
0 1 2 3 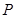
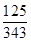

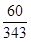
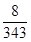
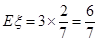 。
。
解析试题分析:(Ⅰ) 优秀 非优秀 总计 甲班 20 90 110 乙班 40 60 100 合计 60 150 210 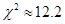 所以按照99%的可靠性要求,能够判断成绩与班级有关 6分
所以按照99%的可靠性要求,能够判断成绩与班级有关 6分
(Ⅱ)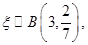 且
且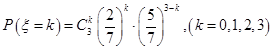 ,
,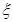 的分布列为
的分布列为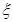
0 1 2 3 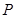
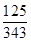

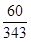
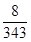
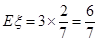 12分
12分
考点:随机变量的分布列及其数学期望,卡方检验。
点评:典型题,统计中的抽样方法,频率直方图,概率计算及分布列问题,是高考必考内容及题型。解答本题的关键之一,是理解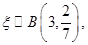 本题对计算能力要求较高。
本题对计算能力要求较高。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
某年某省有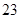 万多文科考生参加高考,除去成绩为
万多文科考生参加高考,除去成绩为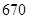 分(含
分(含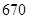 分)以上的
分)以上的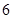 人与成绩为
人与成绩为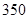 分(不含
分(不含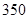 分)以下的
分)以下的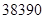 人,还有约
人,还有约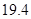 万文科考生的成绩集中在
万文科考生的成绩集中在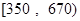 内,其成绩的频率分布如下表所示:
内,其成绩的频率分布如下表所示:
| 分数段 | 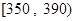 | 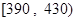 | 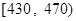 | 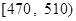 |
| 频率 | 0.108 | 0.133 | 0.161 | 0.183 |
| 分数段 | 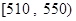 | 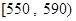 | 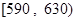 | 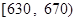 |
| 频率 | 0.193 | 0.154 | 0.061 | 0.007 |
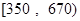 内文科考生的平均分(精确到
内文科考生的平均分(精确到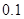 );
);(2)考生A填报志愿后,得知另外有4名同分数考生也填报了该志愿.若该志愿计划录取2人,并在同分数考生中随机录取,求考生A被该志愿录取的概率.
(参考数据:610×0.061+570×0.154+530×0.193+490×0.183+450×0.161+410×0.133=443.93)
“中国式过马路”存在很大的交通安全隐患.某调查机构为了解路人对“中国式过马路 ”的态度是否与性别有关,从马路旁随机抽取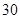 名路人进行了问卷调查,得到了如下列联表:
名路人进行了问卷调查,得到了如下列联表:
| | 男性 | 女性 | 合计 |
| 反感 | 10 | | |
| 不反感 | | 8 | |
| 合计 | | | 30 |
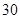 人中随机抽取
人中随机抽取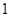 人抽到反感“中国式过马路 ”的路人的概率是
人抽到反感“中国式过马路 ”的路人的概率是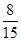 .
.(Ⅰ)请将上面的列联表补充完整(在答题卷上直接填写结果,不需要写求解过程),并据此资料判断是否有95%的把握认为反感“中国式过马路 ”与性别有关?
(Ⅱ)若从这
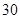 人中的女性路人中随机抽取
人中的女性路人中随机抽取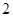 人参加一活动,记反感“中国式过马路”的人数为
人参加一活动,记反感“中国式过马路”的人数为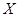 ,求
,求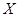 的分布列.
的分布列. 附:
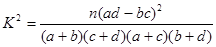 ,其中
,其中 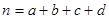
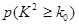 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
某兴趣小组欲研究昼夜温差大小与患感冒人数多少之间的关系,他们分别到气象局与某医院抄录了1至6月份每月10号的昼夜温差情况与因患感冒而就诊的人数,得到如下资料:
| 日 期 | 1月10日 | 2月10日 | 3月10日 | 4月10日 | 5月10日 | 6月10日 |
| 昼夜温差x(°C) | 10 | 11 | 13 | 12 | 8 | 6 |
| 就诊人数y(个) | 22 | 25 | 29 | 26 | 16 | 12 |
线性回归方程,再用被选取的2组数据进行检验.
(Ⅰ)求选取的2组数据恰好是相邻两个月的概率;
(Ⅱ)若选取的是1月与6月的两组数据,请根据2至5月份的数据,求出y关于x
的线性回归方程
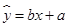 ;
; (Ⅲ)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2
人,则认为得到的线性回归方程是理想的,试问该小组所得线性回归方程是否理
想?
(参考公式:
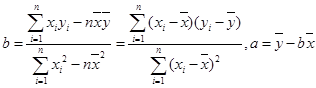 )
) 为了了解初三学生女生身高情况,某中学对初三女生身高进行了一次测量,所得数据整理后列出了频率分布表如下:
| 组 别 | 频数 | 频率 |
| [145.5,149.5) | 1 | 0.02 |
| [149.5,153.5) | 4 | 0.08 |
| [153.5,157.5) | 20 | 0.40 |
| [157.5,161.5) | 15 | 0.30 |
| [161.5,165.5) | 8 | 0.16 |
| [165.5,169.5) | m | n |
| 合 计 | M | N |
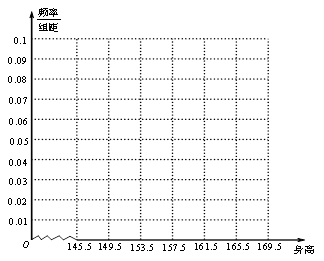
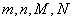 所表示的数;
所表示的数;(2)画出频率分布直方图;
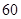 名,将其成绩(均为整数)整理后画出的频率分布直方图如下:观察图形,回答下列问题:
名,将其成绩(均为整数)整理后画出的频率分布直方图如下:观察图形,回答下列问题: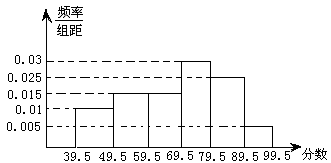
 这一组的频数、频率分别是多少?
这一组的频数、频率分别是多少?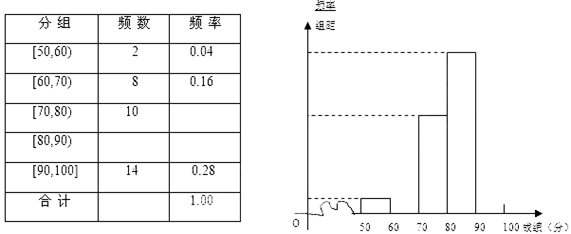
 段的有多少人;
段的有多少人;