题目内容
如图所示,在正方体ABCD﹣A1B1C1D1中,棱长AB=1.
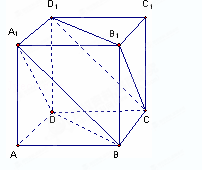
(Ⅰ)求异面直线A1B与 B1C所成角的大小;(Ⅱ)求证:平面A1BD∥平面B1CD1.

(Ⅰ)求异面直线A1B与 B1C所成角的大小;(Ⅱ)求证:平面A1BD∥平面B1CD1.
(Ⅰ)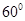 (Ⅱ)见解析
(Ⅱ)见解析
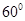 (Ⅱ)见解析
(Ⅱ)见解析试题分析:(Ⅰ)根据异面直线所成角的定义,易知图中
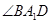 就为所求角,又三角形
就为所求角,又三角形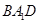 为正三角形;(Ⅱ)根据面面平行的判定定理,要证平面A1BD∥平面B1CD 1 可转化为两相交直线BD和A1B平行于平面B1CD 1,而直线与平面平行又可转化为直线与直线平行角的处理其中很关键的一步就是落实角,而异面直线所成角,往往就是通过平移其中的一条直线或两条直线转化为相交位置出现角,再结合平面几何知识进行求解;空间位置关系的证明,其核心就是转化化归,本小题中线线平行、线面平行和面面平行之间在不断的转化.
为正三角形;(Ⅱ)根据面面平行的判定定理,要证平面A1BD∥平面B1CD 1 可转化为两相交直线BD和A1B平行于平面B1CD 1,而直线与平面平行又可转化为直线与直线平行角的处理其中很关键的一步就是落实角,而异面直线所成角,往往就是通过平移其中的一条直线或两条直线转化为相交位置出现角,再结合平面几何知识进行求解;空间位置关系的证明,其核心就是转化化归,本小题中线线平行、线面平行和面面平行之间在不断的转化.试题解析:(Ⅰ)因为B1C//A1D,所以
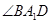 为异面直线A1B与B1C所成角。在
为异面直线A1B与B1C所成角。在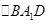 中,易得
中,易得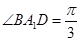
(Ⅱ)
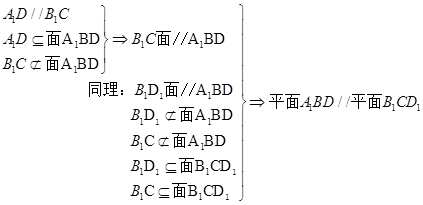

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
 中,底面
中,底面 是直角梯形,
是直角梯形, ,
, ,
,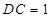 ,
,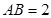 ,
,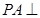 平面
平面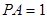 .
. 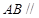 平面
平面 ;
; 平面
平面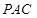 ;
;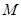 是
是 的中点,求三棱锥
的中点,求三棱锥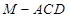 的体积.
的体积.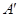 .
.
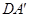 ⊥EF;
⊥EF;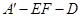 的平面角的余弦值.
的平面角的余弦值.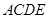 所在的平面垂直于平面
所在的平面垂直于平面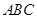 ,
,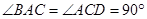 ,
,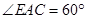 ,
,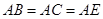 .
.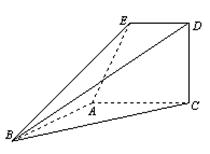
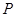 是直线
是直线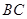 中点,证明
中点,证明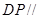 平面
平面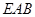 ;
;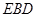 与平面
与平面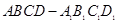 中,
中,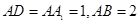 ,点E是AB的中点.
,点E是AB的中点.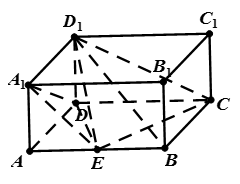
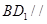 平面
平面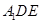 ;
;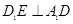 ;
;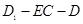 的正切值.
的正切值.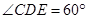 ,M是DE的中点,F是AC的中点,且AC=4,
,M是DE的中点,F是AC的中点,且AC=4,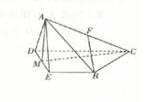
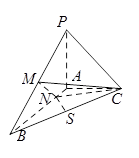
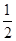 AB,
AB,