题目内容
(本题满分10分)已知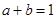 ,对
,对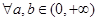 ,
,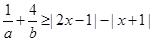 恒成立,求
恒成立,求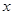 的取值范围。
的取值范围。
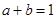 ,对
,对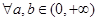 ,
,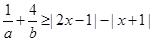 恒成立,求
恒成立,求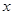 的取值范围。
的取值范围。-7≤x≤11
本试题主要是考查了不等式中绝对值不等式的恒成立问题的运用,以及均值不等式的综合求解。,根据>0,b>0 且a+b="1" ,对于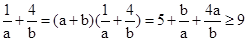 ,下一步就是求解绝对值不等式即可。
,下一步就是求解绝对值不等式即可。
解:∵ a>0,b>0 且a+b="1" ∴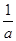 +
+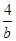 ="(a+b)("
="(a+b)(" 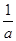 +
+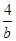 )=5+
)=5+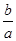 +
+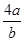 ≥9,
≥9,
故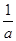 +
+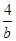 的最小值为9, ------------------------5分
的最小值为9, ------------------------5分
因为对a,b∈(0,+∞),使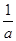 +
+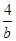 ≥|2x-1|-|x+1|恒成立,所以,|2x-1|-|x+1|≤9, -7分
≥|2x-1|-|x+1|恒成立,所以,|2x-1|-|x+1|≤9, -7分
当 x≤-1时,2-x≤9, ∴ -7≤x≤-1, 当 -1<x<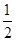 时,-3x≤9,
时,-3x≤9,
∴ -1<x<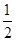 ,当 x≥
,当 x≥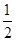 时,x-2≤9, ∴
时,x-2≤9, ∴ 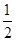 ≤x≤11,∴ -7≤x≤11 ------------- 10分
≤x≤11,∴ -7≤x≤11 ------------- 10分
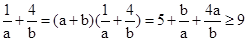 ,下一步就是求解绝对值不等式即可。
,下一步就是求解绝对值不等式即可。解:∵ a>0,b>0 且a+b="1" ∴
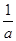 +
+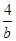 ="(a+b)("
="(a+b)(" 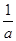 +
+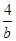 )=5+
)=5+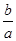 +
+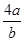 ≥9,
≥9,故
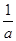 +
+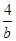 的最小值为9, ------------------------5分
的最小值为9, ------------------------5分因为对a,b∈(0,+∞),使
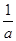 +
+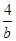 ≥|2x-1|-|x+1|恒成立,所以,|2x-1|-|x+1|≤9, -7分
≥|2x-1|-|x+1|恒成立,所以,|2x-1|-|x+1|≤9, -7分当 x≤-1时,2-x≤9, ∴ -7≤x≤-1, 当 -1<x<
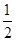 时,-3x≤9,
时,-3x≤9, ∴ -1<x<
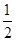 ,当 x≥
,当 x≥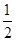 时,x-2≤9, ∴
时,x-2≤9, ∴ 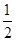 ≤x≤11,∴ -7≤x≤11 ------------- 10分
≤x≤11,∴ -7≤x≤11 ------------- 10分
练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
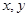 ,满足
,满足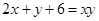 ,则
,则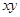 的最小值是 __ .
的最小值是 __ .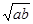
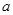 b
b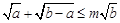 恒成立,则m的最小值是 。
恒成立,则m的最小值是 。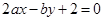
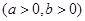 被圆
被圆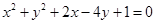 截得的弦长为4,则
截得的弦长为4,则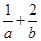 的最小值为___________.
的最小值为___________.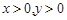 ,且
,且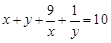 ,则
,则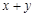 的最大值为 .
的最大值为 .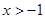 ,则当且仅当
,则当且仅当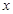 = 时,函数
= 时,函数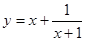 的最大值
的最大值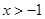 ,求
,求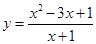 的最小值为
的最小值为 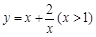 的值域为( )
的值域为( )