Question

想象一下一个人从出生到死亡，在每个生日都测量身高，并作出这些数据散点图，这些点将不会落在一条直线上，但在一段时间内的增长数据有时可以用线性回归来分析.下表是一位母亲给儿子作的成长记录：

年龄/周岁	3	4	5	6	7	8	9
身高/cm	90.8	97.6	104.2	110.9	115.6	122.0	128.5
年龄/周岁	10	11	12	13	14	15	16
身高/cm	134.2	140.8	147.6	154.2	160.9	167.5	173.0

（1）年龄（解释变量）和身高（预报变量）之间具有怎样的相关关系？

（2）如果年龄相差5岁，则身高有多大差异？（3～16岁之间）

（3）如果身高相差20 cm，其年龄相差多少？

（4）计算残差，说明该函数模型能够较好地反映年龄与身高的关系吗？请说明理由?

Answer 1

解：设年龄x与身高Y之间的回归直线方程?

（1）=bx+a，?

由公式b=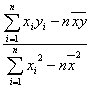≈6.317，?

a=-b=71.984,?

所以=6.317x+71.984.??

（2）如果年龄相差5岁,则预报变量变化6.317×5=31.585.?

（3）如果身高相差20 cm,年龄相差?

Δx==3.166≈3.?

（4）=≈4.59,

=≈7 227.2,?

Y	90.8	97.6	104.2	110.9	115.6	122.0	128.5
	90.9	97.3	103.6	109.9	116.2	122.5	128.8
Y	134.2	140.8	147.6	154.2	160.9	167.5	173.0
	135.2	141.5	147.8	154.1	160.4	166.7	173.1

R²≈0.999,?

所以残差平方和为4.59，相关指数为0.999，故该函数模型能够较好地反映年龄与身高的关系?

点评:残差平方和所占比例越小，相关指数（即回归平方和所占比例）越大,函数模型越能较好地反映X与Y的关系.