题目内容
设函数f(x)=aex+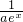 +b(a>0).
+b(a>0).
(Ⅰ)求f(x)在[0,+∞)内的最小值;
(Ⅱ)设曲线y=f(x)在点(2,f(2))处的切线方程为y=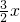 ,求a,b的值.
,求a,b的值.
解:(Ⅰ)设t=ex(t≥1),则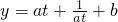
∴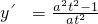
①当a≥1时,y′>0,∴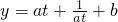 在t≥1上是增函数,
在t≥1上是增函数,
∴当t=1(x=0)时,f(x)的最小值为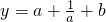
②当0<a<1时,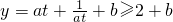 ,当且仅当at=1(x=-lna)时,f(x)的最小值为b+2;
,当且仅当at=1(x=-lna)时,f(x)的最小值为b+2;
(Ⅱ)求导函数,可得)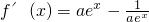
∵曲线y=f(x)在点(2,f(2))处的切线方程为y=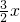 ,
,
∴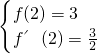 ,即
,即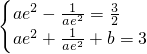 ,解得
,解得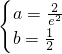 .
.
分析:(Ⅰ)设t=ex(t≥1),则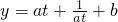 ,求出导函数
,求出导函数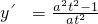 ,再进行分类讨论:①当a≥1时,y′>0,
,再进行分类讨论:①当a≥1时,y′>0,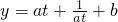 在t≥1上是增函数;②当0<a<1时,利用基本不等式
在t≥1上是增函数;②当0<a<1时,利用基本不等式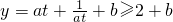 ,当且仅当at=1(x=-lna)时,f(x)取得最小值;
,当且仅当at=1(x=-lna)时,f(x)取得最小值;
(Ⅱ)求导函数,利用曲线y=f(x)在点(2,f(2))处的切线方程为y=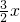 ,建立方程组,即可求得a,b的值.
,建立方程组,即可求得a,b的值.
点评:本题考查导数知识的运用,考查导数的几何意义,考查函数的单调性与最值,属于中档题.
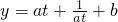
∴
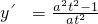
①当a≥1时,y′>0,∴
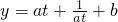 在t≥1上是增函数,
在t≥1上是增函数,∴当t=1(x=0)时,f(x)的最小值为
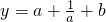
②当0<a<1时,
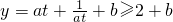 ,当且仅当at=1(x=-lna)时,f(x)的最小值为b+2;
,当且仅当at=1(x=-lna)时,f(x)的最小值为b+2;(Ⅱ)求导函数,可得)
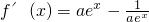
∵曲线y=f(x)在点(2,f(2))处的切线方程为y=
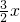 ,
,∴
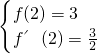 ,即
,即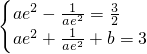 ,解得
,解得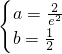 .
.分析:(Ⅰ)设t=ex(t≥1),则
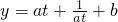 ,求出导函数
,求出导函数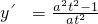 ,再进行分类讨论:①当a≥1时,y′>0,
,再进行分类讨论:①当a≥1时,y′>0,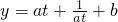 在t≥1上是增函数;②当0<a<1时,利用基本不等式
在t≥1上是增函数;②当0<a<1时,利用基本不等式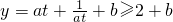 ,当且仅当at=1(x=-lna)时,f(x)取得最小值;
,当且仅当at=1(x=-lna)时,f(x)取得最小值;(Ⅱ)求导函数,利用曲线y=f(x)在点(2,f(2))处的切线方程为y=
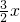 ,建立方程组,即可求得a,b的值.
,建立方程组,即可求得a,b的值.点评:本题考查导数知识的运用,考查导数的几何意义,考查函数的单调性与最值,属于中档题.

练习册系列答案
相关题目
 (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分.)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分.)