题目内容
设 是一个公差为2的等差数列,
是一个公差为2的等差数列, 成等比数列.
成等比数列.
(1) 求数列 的通项公式
的通项公式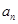 ;
;
(2) 数列 满足
满足 ,设
,设 的前n项和为
的前n项和为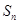 ,求
,求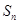 .
.
解:(Ⅰ)由a1,a2,a4成等比数列得:(a1+2)2=a1(a1+6). -------------------- 2分
解得a1=2…4分 数列{an}的通项公式是an=2n(n∈N*) ------------------6分
(Ⅱ)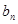 =n·22n?=n·4n(n∈N*)Sn=1·4+2·42+…+n·4n ①4Sn=1·42+…+(n-1)4n+n4n+1②, ①-②得-3Sn=
=n·22n?=n·4n(n∈N*)Sn=1·4+2·42+…+n·4n ①4Sn=1·42+…+(n-1)4n+n4n+1②, ①-②得-3Sn=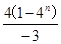 -n·4n+1?,即Sn=
-n·4n+1?,即Sn=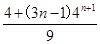 -----------12分
-----------12分
解析

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
各项都为正数的等比数列 中,
中,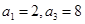 ,则公比
,则公比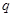 的值为( )
的值为( )
| A.2 | B.3 | C.4 | D.5 |
在等比数列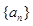 中,若
中,若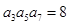 ,则
,则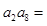 ( )
( )
| A.4 | B.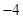 | C.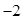 | D.2 |
 是等差数列,
是等差数列,
 ,求数列
,求数列 的前n项和Sn.
的前n项和Sn. 是首项为
是首项为 ,公差为
,公差为 的等差数列,其前
的等差数列,其前 项和为
项和为 ,且
,且 成等差数列.
成等差数列. 的前
的前 ,求
,求 的公比
的公比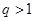 ,
, 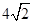 是
是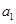 和
和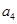 的一个等比中项,
的一个等比中项,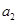 和
和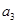 的等差中项为
的等差中项为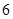 ,若数列
,若数列 满足
满足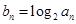 (
(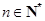 ).
).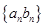 的前
的前 项和
项和 .
. 的前
的前 项和为
项和为 ,且
,且
 的通项公式
的通项公式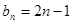 ,记
,记 ,求数列
,求数列 的前
的前 .
.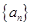 满足:
满足: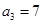 ,
,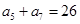 ,
, .
.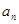 及
及 (
(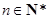 ),求数列
),求数列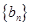 的前n项和
的前n项和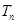 .
.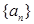 是等差数列,且
是等差数列,且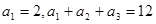 .
.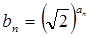 ,求数列
,求数列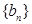 的前10项和.
的前10项和.