题目内容
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,四个顶点构成的菱形的面积是4,圆
,四个顶点构成的菱形的面积是4,圆![]() 过椭圆
过椭圆![]() 的上顶点
的上顶点![]() 作圆
作圆![]() 的两条切线分别与椭圆
的两条切线分别与椭圆![]() 相交于
相交于![]() 两点(不同于点
两点(不同于点![]() ),直线
),直线![]() 的斜率分别为
的斜率分别为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)当![]() 变化时,①求
变化时,①求![]() 的值;②试问直线
的值;②试问直线![]() 是否过某个定点?若是,求出该定点;若不是,请说明理由.
是否过某个定点?若是,求出该定点;若不是,请说明理由.
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】试题分析:(1)由题设知, ![]() ,
, ![]() ,又
,又![]() ,解得
,解得![]() ,由此可得求椭圆
,由此可得求椭圆![]() 的方程;(2)①
的方程;(2)①![]() ,则有
,则有 ,化简得
,化简得![]() ,对于直线
,对于直线![]() ,同理有
,同理有![]() ,于是
,于是![]() 是方程
是方程![]() 的两实根,故
的两实根,故![]() ,即可证明结果;②考虑到
,即可证明结果;②考虑到![]() 时,
时, ![]() 是椭圆的下顶点,
是椭圆的下顶点, ![]() 趋近于椭圆的上顶点,故
趋近于椭圆的上顶点,故![]() 若过定点,则猜想定点在
若过定点,则猜想定点在![]() 轴上.
轴上.
由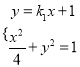 ,得
,得![]() ,于是有
,于是有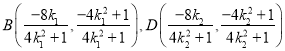 ,直线
,直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的方程为
的方程为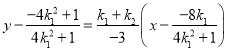 ,令
,令![]() ,得
,得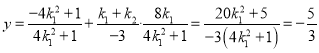 ,即可证明直线
,即可证明直线![]() 过定点.
过定点.
试题解析:(1)由题设知, ![]() ,
, ![]() ,又
,又![]() ,
,
解得![]() .
.
故所求椭圆![]() 的方程是
的方程是![]() .
.
(2)①![]() ,则有
,则有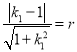 ,化简得
,化简得![]() ,
,
对于直线![]() ,同理有
,同理有![]() ,
,
于是![]() 是方程
是方程![]() 的两实根,故
的两实根,故![]() .
.
考虑到![]() 时,
时, ![]() 是椭圆的下顶点,
是椭圆的下顶点, ![]() 趋近于椭圆的上顶点,故
趋近于椭圆的上顶点,故![]() 若过定点,则猜想定点在
若过定点,则猜想定点在![]() 轴上.
轴上.
由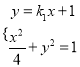 ,得
,得![]() ,于是有
,于是有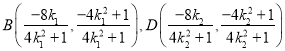 .
.
直线![]() 的斜率为
的斜率为![]() ,
,
直线![]() 的方程为
的方程为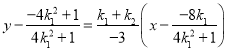 ,
,
令![]() ,得
,得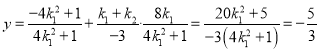 ,
,
故直线![]() 过定点
过定点![]() .
.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
