题目内容
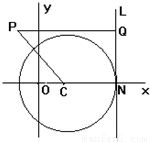
已知圆C方程:(x-1)2 + y 2=9,垂直于x轴的直线L与圆C相切于N点(N在圆心C的右侧),平面上有一动点P,若PQ⊥L,垂足为Q,且 ;
;
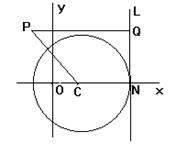
(1)求点P的轨迹方程;
(2)已知D为点P的轨迹曲线上第一象限弧上一点,O为原点,A、B分别为点P的轨迹曲线与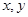 轴的正半轴的交点,求四边形OADB的最大面积及D点坐标.
轴的正半轴的交点,求四边形OADB的最大面积及D点坐标.
【答案】
(1)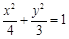 (2)四边形
(2)四边形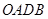 的最大面积为
的最大面积为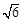 ,
,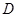 点坐标为
点坐标为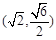
【解析】(1)设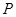 点坐标为
点坐标为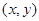 ,然后对其
,然后对其 坐标化,然后化简即可求得点P的轨迹方程.
坐标化,然后化简即可求得点P的轨迹方程.
(2)本小题为研究方便,可以设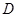 点坐标为
点坐标为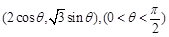
然后再四边形OADB的面积表示成关于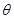 的三角函数求研究其最值.
的三角函数求研究其最值.
解:(1)设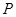 点坐标为
点坐标为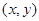 ,…………………1分
,…………………1分
则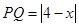 ,……………2分
,……………2分
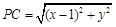 …………………………3分
…………………………3分
因为 ,所以
,所以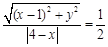 ,
…………………4分
,
…………………4分
化简得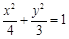 ………………………………5分
………………………………5分
所以点 的轨迹方程是
的轨迹方程是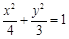 ………………6分
………………6分
(2)依题意得,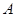 点坐标为
点坐标为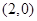 ,
,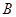 点坐标为
点坐标为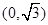 ……………7分
……………7分
设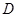 点坐标为
点坐标为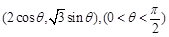 ,……………8分
,……………8分
则四边形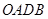 的面积
的面积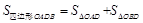 ,………………………9分
,………………………9分
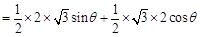 ………………10分
………………10分
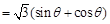
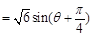 …………………11分
…………………11分
又因为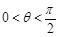 ,所以
,所以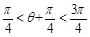 …………………………12分
…………………………12分
所以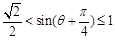 ,即
,即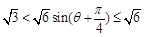
所以四边形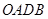 的最大面积为
的最大面积为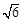 ,………………………………………13分
,………………………………………13分
当四边形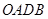 的面积取最大时,
的面积取最大时,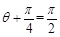 ,即
,即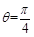 ,
,
此时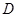 点坐标为
点坐标为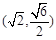 ………………………………………………………………14分
………………………………………………………………14分

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案
相关题目
 (2012•珠海二模)已知圆C方程:(x-1)2+y2=9,垂直于x轴的直线L与圆C相切于N点(N在圆心C的右侧),平面上有一动点P,若PQ⊥L,垂足为Q,且
(2012•珠海二模)已知圆C方程:(x-1)2+y2=9,垂直于x轴的直线L与圆C相切于N点(N在圆心C的右侧),平面上有一动点P,若PQ⊥L,垂足为Q,且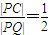 ;
;
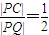 ;
;