题目内容
已知圆C方程为：(x－2m－1)2＋(y－m－1)2＝4m2(m≠0)
(1)求证：当m变化时，圆C的圆心在一定直线上；
(2)求(1)中一系列圆的公切线的方程．
答案：
解析：
解析：
(1)[证明]由
消去m得a－2b＋1＝0．故这些圆的圆心在直线x－2y＋1＝0上．(2)设公切线方程为y＝kx＋b，则由相切有2|m|＝
，对一切m≠0成立．即(－4k－3)m2＋2(2k－1)(k＋b－1)m＋(k＋b－1)2＝0对一切m≠0恒成立
所以
即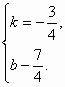
当k不存在时直线为x＝1．所以公切线方程y＝
和x＝1．
练习册系列答案
相关题目