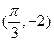题目内容
将函数 进行平移,使得到的图形与抛物线
进行平移,使得到的图形与抛物线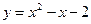 的两个交点关于原点对称,试求平移后的图形对应的函数解析式.
的两个交点关于原点对称,试求平移后的图形对应的函数解析式.
 进行平移,使得到的图形与抛物线
进行平移,使得到的图形与抛物线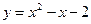 的两个交点关于原点对称,试求平移后的图形对应的函数解析式.
的两个交点关于原点对称,试求平移后的图形对应的函数解析式.函数解析式是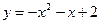
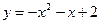
设出平移公式,用待定系数表示出平移后对应的函数解析式,将其与已知抛物线方程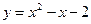 联立,即能利用交点关于原点对称的条件建立方程组求出待定系数:
联立,即能利用交点关于原点对称的条件建立方程组求出待定系数:
设平移向量是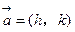 ,则平移公式即
,则平移公式即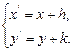
∴平移后的函数解析式是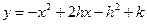 ,
,
与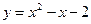 联立,消去
联立,消去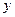 得
得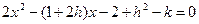 ,
,
由于两交点关于原点对称,∴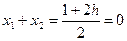 ,即
,即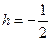 ,
,
又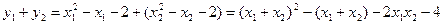 ,
,
∴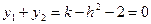 ,
,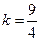 ,
,
所求的函数解析式是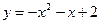 .
.
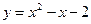 联立,即能利用交点关于原点对称的条件建立方程组求出待定系数:
联立,即能利用交点关于原点对称的条件建立方程组求出待定系数:设平移向量是
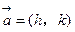 ,则平移公式即
,则平移公式即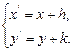
∴平移后的函数解析式是
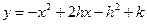 ,
,与
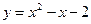 联立,消去
联立,消去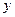 得
得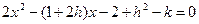 ,
,由于两交点关于原点对称,∴
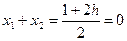 ,即
,即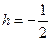 ,
,又
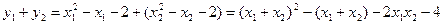 ,
,∴
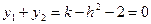 ,
,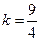 ,
,所求的函数解析式是
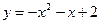 .
.
练习册系列答案
相关题目
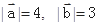 .(1)若
.(1)若 的夹角为60o,求
的夹角为60o,求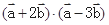 ;
;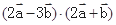 =61,求
=61,求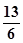 ,求sinθ+cosθ的值;(2)若a//b,求sin(2θ+
,求sinθ+cosθ的值;(2)若a//b,求sin(2θ+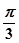 )的值.
)的值. ,
, 共线的充要条件是( )
共线的充要条件是( ) ,
,
 ,
,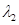 ,
,
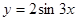 变为曲线
变为曲线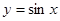 的伸缩变换是( )
的伸缩变换是( )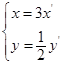
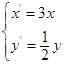
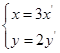
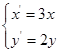
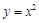 的图象F按向量
的图象F按向量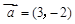 平移到
平移到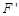 ,则
,则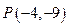 、
、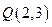 且
且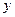 轴与线段
轴与线段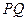 的交点为
的交点为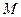 ,则点
,则点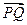 所成的比为 ( )
所成的比为 ( )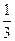
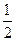
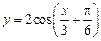 的图象按向量
的图象按向量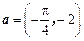 平移,则平移后所得图象的解析式为( )
平移,则平移后所得图象的解析式为( )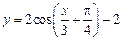
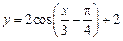
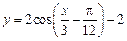
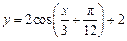
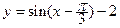 的图象经过按
的图象经过按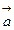 平移得到
平移得到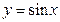 的图象,则
的图象,则