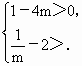题目内容
已知函数![]() ,(x>0).
,(x>0).
(Ⅰ)当0<a<b,且f(a)=f(b)时,求证:ab>1;
(Ⅱ)是否存在实数a,b(a<b),使得函数y=f(x)的定义域、值域都是[a,b],若存在,则求出a,b的值,若不存在,请说明理由.
(Ⅲ)若存在实数a,b(a<b),使得函数y=f(x)的定义域为[a,b]时,值域为[ma,mb]
(m≠0),求m的取值范围.
解析:
|
解:(Ⅰ)∵x>0,∴ ∴f(x)在(0,1)上为减函数,在 由0<a<b,且f(a)=f(b), 可得0<a<1<b和 即 ∴2ab=a+b> 故 (Ⅱ)不存在满足条件的实数a,b. 若存在满足条件的实数a,b,使得函数y= 当 故 解得a=b. 故此时不存在适合条件的实数a,b. 6分 当 故 此时a,b是方程 故此时不存在适合条件的实数a,b. 8分 当 由于 故此时不存在适合条件的实数a,b. 综上可知,不存在适合条件的实数a,b. 10分 (Ⅲ)若存在实数a,b(a<b),使得函数y=f(x)的定义域为[a,b]时,值域为[ma,mb]. 则a>0,m>0. 当 当 故只有 ∵ ∴ b是方程 即关于x的方程 设这两个根为 则 ∴ 解得 故m的取值范围是 |

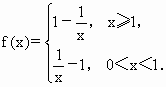

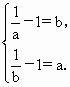

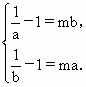 .此时刻得a,b异号,不符合题意,所以a,b不存在.
.此时刻得a,b异号,不符合题意,所以a,b不存在.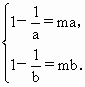
 即
即