题目内容
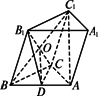
如图,各棱长都等于2的斜三棱柱AC-A1B1C1中,侧面ABB1A1垂直于底面.

(1)侧棱与底面所成角为多少时,能使B1C⊥AC1;
(2)在(1)的条件下求此三棱柱的侧面积.
答案:
解析:
解析:
|
(1)当侧棱与底面所成角为60°时,能使B1C⊥AC1.事实上,作B1D⊥AB于点D.
∵面ABB1A1⊥底面ABC, ∴B1D⊥平面ABC. ∴∠B1BD为侧棱BB1与底面所成角. ∴∠B1BD=60°. 又BD=B1Ecos60°=1, ∴D为AB中点. ∴CD= 又B1D= 又O为B1C中点,∴DO⊥B1C.而AC1∥DO, ∴AC1⊥B1C. (2)在侧面ABB1A1中, 在△B1CD中,CD= 又BCC1B1为菱形, ∴BC1=2BO= 又AB⊥面B1CD,∴AB⊥DO. 又DO∥AC1,∴AC1⊥AB. 在Rt△ABC1中,AC1= ∴ ∴S侧= |

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案
相关题目
 如图,正三棱柱ABC-A1B1C1的各棱长都等于2,D在AC1上,F为BB1中点,且FD⊥AC1.
如图,正三棱柱ABC-A1B1C1的各棱长都等于2,D在AC1上,F为BB1中点,且FD⊥AC1. 如图,正三棱柱ABC-A1B1C1的各棱长都等于2,D在AC1上,F为BB1中点,且FD⊥AC1.
如图,正三棱柱ABC-A1B1C1的各棱长都等于2,D在AC1上,F为BB1中点,且FD⊥AC1.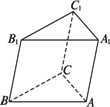

 的值;
的值;