题目内容
【题目】在平面直角坐标系xoy中,过椭圆 ![]() 右焦点的直线
右焦点的直线 ![]() 交椭圆C于M,N两点,P为M,N的中点,且直线OP的斜率为
交椭圆C于M,N两点,P为M,N的中点,且直线OP的斜率为 ![]() .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设另一直线l与椭圆C交于A,B两点,原点O到直线l的距离为 ![]() ,求△AOB面积的最大值.
,求△AOB面积的最大值.
【答案】解:(Ⅰ)由题意,直线 ![]() 与x轴交点F(
与x轴交点F( ![]() ,0),则c=
,0),则c= ![]() , 设M(x1 , y1)、N(x2 , y2),P(xP , yP),2xP=x1+x2 , 2yP=y1+y2 ,
, 设M(x1 , y1)、N(x2 , y2),P(xP , yP),2xP=x1+x2 , 2yP=y1+y2 ,
直线OP的斜率k= ![]() ,
,
则: 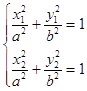 ,
,
整理得: ![]() +
+ ![]() =0,
=0,
则 ![]() =﹣
=﹣ ![]() =﹣
=﹣ ![]() ,
,
由直线MN的斜率k= ![]() =﹣
=﹣ ![]() ×3=﹣1,整理得:a2=3b2=3(a2﹣c2),
×3=﹣1,整理得:a2=3b2=3(a2﹣c2),
又c= ![]() ,解得:a2=3,b2=1,
,解得:a2=3,b2=1,
∴椭圆C的方程为: ![]() ;
;
(Ⅱ)由题意,①当直线l的斜率不存在时,O到直线l的距离为 ![]() ,
,
将x=± ![]() 代入椭圆方程,解得:y=±
代入椭圆方程,解得:y=± ![]() ,则丨AB丨=2丨y丨=
,则丨AB丨=2丨y丨= ![]() ;
;
当直线斜率为O时,将y=± ![]() ,代入椭圆方程,解得:x=±
,代入椭圆方程,解得:x=± ![]() ,
,
则丨AB丨=2丨x丨= ![]() ;
;
②当直线l的斜率存在时且不为0时,
设直线l的方程为:y=kx+m(k,m∈R且k≠0),
由题意,原点0到直线l的距离为 ![]() ,
,
故 ![]()
![]() ,则m2=
,则m2= ![]() (k2+1).
(k2+1).
设A(x1 , y1)、B(x2 , y2),
则: 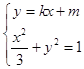 ,(1+3k2)x2+6kmx+3(m2﹣1)=,
,(1+3k2)x2+6kmx+3(m2﹣1)=,
由题意△>0,x1+x2=﹣ ![]() ,x1x2=
,x1x2= ![]() .
.
丨AB丨2=(1+k2)[(x1+x2)﹣4x1x2]=(1+k2)[(﹣ ![]() )2﹣4×
)2﹣4× ![]() ],
],
=(1+k2) 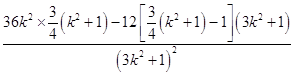 ,
,
= 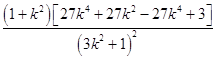 ,
,
= ![]() =3+
=3+ ![]() ,
,
=3+ 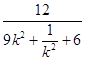 ≤3+
≤3+ ![]() =4,
=4,
当且仅当9k2= ![]() ,即k=±
,即k=± ![]() 时等号成立,丨AB丨max=2,
时等号成立,丨AB丨max=2,
综上所述,当直线l的斜率k=± ![]() 时,
时,
即丨AB丨max=2时,△AOB面积的最大值,
最大值为S= ![]() ×丨AB丨max×
×丨AB丨max× ![]() =
= ![]() ,
,
△AOB面积的最大值 ![]() .
.
【解析】(Ⅰ)当y=0时,求得焦点F坐标,M,N代入椭圆方程,作差,利用中点坐标公式,化简求得MN的直线方程,即可求得a和b的关系,求得椭圆方程;(Ⅱ)由题意可知:当丨AB丨最大时,△AOB面积的最大值,将直线AB代入椭圆方程,利用韦达定理弦长公式及基本不等式的性质,即可求得丨AB丨的最大值.
【考点精析】本题主要考查了椭圆的标准方程的相关知识点,需要掌握椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() 才能正确解答此题.
才能正确解答此题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案