题目内容
设集合A={(x,y)|y≥|x-1|},B={(x,y)|y≤-|x|+a},A∩B≠¢.
(Ⅰ)实数a的取值范围是 ;
(Ⅱ)当a=3时,若(x,y)∈A∩B,则2x+y的最大值是 .
(Ⅰ)实数a的取值范围是
(Ⅱ)当a=3时,若(x,y)∈A∩B,则2x+y的最大值是
分析:(Ⅰ)作出不等式对应的平面区域,根据条件A∩B≠∅,即可求出实数a的取值范围.
(Ⅱ)当a=3时,作出不等式对应的平面区域,利用线性规划的知识求2x+y的最大值.
(Ⅱ)当a=3时,作出不等式对应的平面区域,利用线性规划的知识求2x+y的最大值.
解答: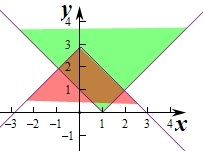 解:(Ⅰ)集合A={(x,y)|y≥|x-1|}表示图中阴影部分(绿色部分),
解:(Ⅰ)集合A={(x,y)|y≥|x-1|}表示图中阴影部分(绿色部分),
集合B={(x,y)|y≤-|x|+a}表示图中阴影部分(红色部分),
∵A∩B≠∅,
∴由图象可知a≥1,
即a的取值范围是[1,+∞).
(Ⅱ)当a=3时,B={(x,y)|y≤-|x|+3},
则A∩B对应的平面区域如图(阴影部分ABCD):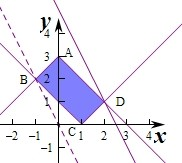
若(x,y)∈A∩B,令z=2x+y,
即y=-2x+z,
平移直线
作直线y=-2x+z,由图知当直线y=-2x+z过D(2,1)时,直线的截距最大,此时z最大.
即z=2×2+1=5.
故答案为:[1,+∞),5.
 解:(Ⅰ)集合A={(x,y)|y≥|x-1|}表示图中阴影部分(绿色部分),
解:(Ⅰ)集合A={(x,y)|y≥|x-1|}表示图中阴影部分(绿色部分),集合B={(x,y)|y≤-|x|+a}表示图中阴影部分(红色部分),
∵A∩B≠∅,
∴由图象可知a≥1,
即a的取值范围是[1,+∞).
(Ⅱ)当a=3时,B={(x,y)|y≤-|x|+3},
则A∩B对应的平面区域如图(阴影部分ABCD):

若(x,y)∈A∩B,令z=2x+y,
即y=-2x+z,
平移直线
作直线y=-2x+z,由图知当直线y=-2x+z过D(2,1)时,直线的截距最大,此时z最大.
即z=2×2+1=5.
故答案为:[1,+∞),5.
点评:本题主要考查二元一次不等式的应用,根据线性规划的知识,利用数形结合是解决本题的关键.

练习册系列答案
相关题目
设集合A=B={(x,y)|x∈R,y∈R},从A到B的映射f:(x,y)→(x+2y,2x-y),则在映射f下B中的元素(1,1)对应的A中元素为( )
| A、(1,3) | ||||
| B、(1,1) | ||||
C、(
| ||||
D、(
|



