题目内容
A是由在[1,4]上有意义且满足如下条件的函数φ(x)组成的集合;
①对任意x∈[1,2],都有φ(2x)∈(1,2);
②存在常数L(0<L<1),使得对任意的x1,x2∈[1,2]都有|φ(2x1)-φ(2x2)|=L|x1-x2|
(1)设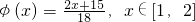 ,证明:φ(x)∈A;
,证明:φ(x)∈A;
(2)设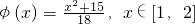 ,是否存在设x0∈(1,2),使得x0=φ(2x0),如存在,求出所有的x0,如不存在请说明理由!
,是否存在设x0∈(1,2),使得x0=φ(2x0),如存在,求出所有的x0,如不存在请说明理由!
证明:(1)因为x∈[1,2],所以φ(2x)=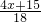 ,x∈[1,2],
,x∈[1,2],
 ≤φ(2x)≤
≤φ(2x)≤ ∴φ(2x)∈(1,2);
∴φ(2x)∈(1,2);
对任意的x1,x2∈[1,2],
|φ(2x1)-φ(2x2)|=| -
- |=
|= ||x1-x2|
||x1-x2|
取L= ∈(0,1),使|φ(2x1)-φ(2x2)|=L||x1-x2|成立
∈(0,1),使|φ(2x1)-φ(2x2)|=L||x1-x2|成立
故φ(x)∈A;
(2)存在x0∈(1,2),使得x0=φ(2x0),
即x0= ,x0∈(1,2),
,x0∈(1,2),
得4x02-18x0+15=0,解得x0=
经检验x0= ∈(1,2),
∈(1,2),
所以存在x0= ∈(1,2),使得x0=φ(2x0).
∈(1,2),使得x0=φ(2x0).
分析:(1)先根据x的范围求出φ(2x)的取值范围,判定是否满足φ(2x)∈(1,2),然后判定是否对任意的x1,x2∈[1,2]都有|φ(2x1)-φ(2x2)|=L|x1-x2|,从而得到结论;
(2)先假设存在,根据x0=φ(2x0)建立方程,然后解方程,最后求出满足条件的x0,从而得到结论.
点评:本题主要考查了函数恒成立问题,以及函数的值域等有关知识,同时考查了计算能力,属于中档题.
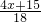 ,x∈[1,2],
,x∈[1,2], ≤φ(2x)≤
≤φ(2x)≤ ∴φ(2x)∈(1,2);
∴φ(2x)∈(1,2);对任意的x1,x2∈[1,2],
|φ(2x1)-φ(2x2)|=|
 -
- |=
|= ||x1-x2|
||x1-x2|取L=
 ∈(0,1),使|φ(2x1)-φ(2x2)|=L||x1-x2|成立
∈(0,1),使|φ(2x1)-φ(2x2)|=L||x1-x2|成立故φ(x)∈A;
(2)存在x0∈(1,2),使得x0=φ(2x0),
即x0=
 ,x0∈(1,2),
,x0∈(1,2),得4x02-18x0+15=0,解得x0=

经检验x0=
 ∈(1,2),
∈(1,2),所以存在x0=
 ∈(1,2),使得x0=φ(2x0).
∈(1,2),使得x0=φ(2x0).分析:(1)先根据x的范围求出φ(2x)的取值范围,判定是否满足φ(2x)∈(1,2),然后判定是否对任意的x1,x2∈[1,2]都有|φ(2x1)-φ(2x2)|=L|x1-x2|,从而得到结论;
(2)先假设存在,根据x0=φ(2x0)建立方程,然后解方程,最后求出满足条件的x0,从而得到结论.
点评:本题主要考查了函数恒成立问题,以及函数的值域等有关知识,同时考查了计算能力,属于中档题.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案
相关题目
 ,证明:φ(x)∈A;
,证明:φ(x)∈A;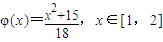 ,是否存在设x∈(1,2),使得x=φ(2x),如存在,求出所有的x,如不存在请说明理由!
,是否存在设x∈(1,2),使得x=φ(2x),如存在,求出所有的x,如不存在请说明理由!