题目内容
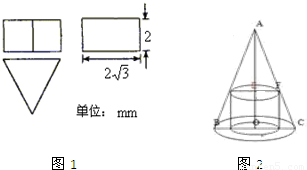
 (1)一个正三棱柱的三视图如图1所示,求这个正三棱柱的表面积?
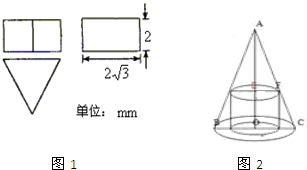
(1)一个正三棱柱的三视图如图1所示,求这个正三棱柱的表面积?(2)已知一个圆锥的底面半径为R(图2),高为3R,求此圆锥内接圆柱表面积的最大值?
分析:(1)三视图复原的几何体是正三棱柱,利用三视图的数据,求解正三棱柱的表面积即可.
(2)将全面积表示成底面半径的函数,用配方法求二次函数的最大值
(2)将全面积表示成底面半径的函数,用配方法求二次函数的最大值
解答:解:(1)三视图复原的几何体是正三棱柱,
S=2×
×(2
)2+3×2
×2
=18
.
(2)设内接圆柱的底面半径为r,高为h,全面积为S,则有
=
∴h=3R-3r
∴S=2πrh+2πr2
=-4πr2+6πRr
=-4π(r2-
Rr)=-4π(r-
R)2+
πR2
∴当r=
R时,S取的最大值
πR2.
所求圆柱的最大值为:
πR2.
S=2×
| ||
| 4 |
| 3 |
| 3 |
=18
| 3 |
(2)设内接圆柱的底面半径为r,高为h,全面积为S,则有
| 3R-h |
| 3R |
| r |
| R |
∴h=3R-3r
∴S=2πrh+2πr2
=-4πr2+6πRr
=-4π(r2-
| 3 |
| 2 |
| 3 |
| 4 |
| 9 |
| 4 |
∴当r=
| 3 |
| 4 |
| 9 |
| 4 |
所求圆柱的最大值为:
| 9 |
| 4 |
点评:本题考查三视图求解几何体的表面积,考查实际问题的最值问题,常转化成函数的最值.

练习册系列答案
相关题目
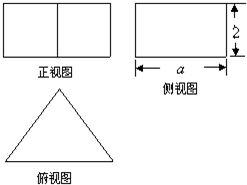 如图是一个正三棱柱的三视图,若三棱柱的体积是1,则a=
如图是一个正三棱柱的三视图,若三棱柱的体积是1,则a=