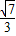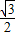题目内容
已知椭圆的焦距、短轴长、长轴长成等差数列，则该椭圆的离心率为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析：先设长轴为2a，短轴为2b，焦距为2c，由题意可知：a+c=2b，由此可以导出该椭圆的离心率．
解答：解：设长轴为2a，短轴为2b，焦距为2c，
则2a+2c=2×2b，
即a+c=2b?（a+c）2=4b2=4（a2-c2）
整理得5e2+2e-3=0，∴e=
或e=-1（舍去），
故选B．
则2a+2c=2×2b，
即a+c=2b?（a+c）2=4b2=4（a2-c2）
整理得5e2+2e-3=0，∴e=
| 3 |
| 5 |
故选B．
点评：本题考查等差数列和椭圆的离心率，难度不大，只需细心运算就行，注意双曲线和椭圆的区别与联系．
练习册系列答案
相关题目
的焦距与短轴长相等，点A，B，C都在椭圆C上，且AB、AC分别过两个焦点F1、F2．
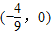，求椭圆方程．
的焦距与短轴长相等，点A，B，C都在椭圆C上，且AB、AC分别过两个焦点F1、F2．
，求椭圆方程．
