题目内容
设动圆M与y轴相切且与圆C：x2+y2-2x=0相外切，则动圆圆心M的轨迹方程为（ ）A．y2=4
B．y2=-4
C．y2=4x或y=0（x＜0）
D．y2=4x或y=0
【答案】分析：设出动圆圆心M的坐标，利用动圆M与y轴相切且与圆C：x2+y2-2x=0相外切，建立方程，化简可得动圆圆心M的轨迹方程．
解答：解：设动圆圆心M的坐标为（x，y），则
∵动圆M与y轴相切且与圆C：x2+y2-2x=0相外切
∴
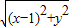=|x|+1
当x＜0时，y=0；当x≥0时，y2=4x
故选C．
点评：本题考查轨迹方程，考查学生的计算能力，属于基础题．
解答：解：设动圆圆心M的坐标为（x，y），则
∵动圆M与y轴相切且与圆C：x2+y2-2x=0相外切
∴
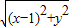=|x|+1当x＜0时，y=0；当x≥0时，y2=4x
故选C．
点评：本题考查轨迹方程，考查学生的计算能力，属于基础题．
练习册系列答案
新课标同步训练系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
（2013•潍坊一模）如图，已知圆C与y轴相切于点T（0，2），与x轴正半轴相交于两点M，N（点M必在点N的右侧），且|MN|=3椭圆D：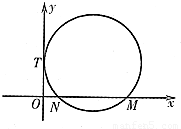
如图，已知圆C与y轴相切于点T（0，2），与x轴正半轴相交于两点M，N（点M必在点N的右侧），且|MN|=3椭圆D：
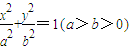的焦距等于2|ON|，且过点
．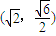