题目内容
设函数
 其中
其中
(Ⅰ)求 的单调区间;
的单调区间;
(Ⅱ) 讨论 的极值.
的极值.
【答案】
(1)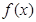 在
在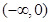 上单调递增;在
上单调递增;在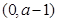 上单调递减;在
上单调递减;在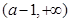 上单调递增.
上单调递增.
(2)当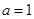 时,函数
时,函数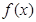 没有极值.当
没有极值.当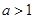 时,函数
时,函数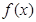 在
在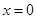 处取得极大值,在
处取得极大值,在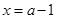 处取得极小值
处取得极小值 .
.
【解析】本试题主要考查了导数的运用。第一问中,求导数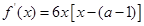 ,然后利用
,然后利用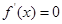 得到方程的根,利用对a=1,
得到方程的根,利用对a=1, 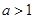 分类讨论可知得到单调区间,第二问中,在(1)的基础上可知
分类讨论可知得到单调区间,第二问中,在(1)的基础上可知
当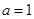 时,函数
时,函数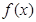 没有极值.
没有极值.
当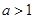 时,函数
时,函数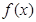 在
在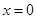 处取得极大值,在
处取得极大值,在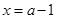 处取得极小值
处取得极小值 ,故得到结论。
,故得到结论。
解:由已知得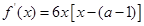 ,令
,令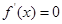 ,解得
,解得 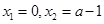 .
.
(Ⅰ)当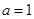 时,
时,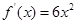 ,
,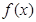 在
在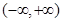 上单调递增
上单调递增
当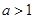 时,
时,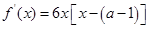 ,
,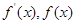 随
随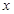 的变化情况如下表:
的变化情况如下表:
|
|
|
0 |
|
|
|
|
|
+ |
0 |
|
0 |
|
|
|
|
极大值 |
|
极小值 |
|
从上表可知,函数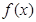 在
在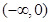 上单调递增;在
上单调递增;在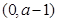 上单调递减;在
上单调递减;在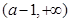 上单调递增.
上单调递增.
(Ⅱ)由(Ⅰ)知,当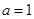 时,函数
时,函数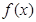 没有极值.
没有极值.
当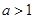 时,函数
时,函数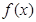 在
在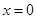 处取得极大值,在
处取得极大值,在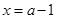 处取得极小值
处取得极小值 .
.

练习册系列答案
相关题目
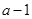
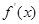
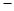
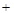
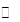
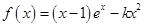 (其中
(其中 ).
). 时,求函数
时,求函数 的单调区间;
的单调区间; 时,求函数
时,求函数 上的最大值
上的最大值 .
.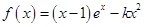 (其中
(其中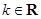 ).
).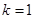 时,求函数
时,求函数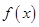 的单调区间和极值;
的单调区间和极值;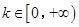 时,函数
时,函数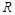 上有且只有一个零点.
上有且只有一个零点.
 其中
其中
 的单调区间;
的单调区间;