题目内容
如果 的三个内角的余弦值分别等于
的三个内角的余弦值分别等于 对应的三个内角的正弦值,则
对应的三个内角的正弦值,则
 的三个内角的余弦值分别等于
的三个内角的余弦值分别等于 对应的三个内角的正弦值,则
对应的三个内角的正弦值,则A. 和 和 均为锐角三角形 均为锐角三角形 |
B. 和 和 均为钝角三角形 均为钝角三角形 |
C. 为钝角三角形, 为钝角三角形, 为锐角三角形 为锐角三角形 |
D. 为锐角三角形, 为锐角三角形, 为钝角三角形 为钝角三角形 |
D
试题分析:首先根据正弦、余弦在(0,π)内的符号特征,确定△A1B1C1是锐角三角形;然后假设△A2B2C2是锐角三角形,则由cosα=sin(
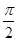 -α)推导出矛盾;再假设△A2B2C2是直角三角形,易于推出矛盾;最后得出△A2B2C2是钝角三角形的结论.解:因为△A2B2C2的三个内角的正弦值均大于0,所以△A1B1C1的三个内角的余弦值也均大于0,则△A1B1C1是锐角三角形.若△A2B2C2是锐角三角形,由sinA2=cosA1=sin(
-α)推导出矛盾;再假设△A2B2C2是直角三角形,易于推出矛盾;最后得出△A2B2C2是钝角三角形的结论.解:因为△A2B2C2的三个内角的正弦值均大于0,所以△A1B1C1的三个内角的余弦值也均大于0,则△A1B1C1是锐角三角形.若△A2B2C2是锐角三角形,由sinA2=cosA1=sin(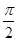 - A1), sinB2=cosB1=sin(
- A1), sinB2=cosB1=sin(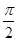 - B1), sinC2=cosC1=sin(
- B1), sinC2=cosC1=sin(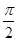 - C1)得,那么,A2+B2+C2=
- C1)得,那么,A2+B2+C2=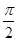 ,这与三角形内角和是π相矛盾;若△A2B2C2是直角三角形,不妨设A2=
,这与三角形内角和是π相矛盾;若△A2B2C2是直角三角形,不妨设A2=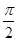 ,则sinA2=1=cosA1,所以A1在(0,π)范围内无值.所以△A2B2C2是钝角三角形.故选D
,则sinA2=1=cosA1,所以A1在(0,π)范围内无值.所以△A2B2C2是钝角三角形.故选D点评:本题主要考查正余弦函数在各象限的符号特征及诱导公式,同时考查反证法思想

练习册系列答案
相关题目
 满足对任意的
满足对任意的 都有
都有 ,
,
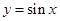 的图像上所有的点向右平行移动
的图像上所有的点向右平行移动 个单位长度,再把所得各点的横坐标伸长到原来的
个单位长度,再把所得各点的横坐标伸长到原来的 倍(纵坐标不变),所得图像的函数解析式是( )
倍(纵坐标不变),所得图像的函数解析式是( )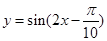



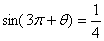 ,
,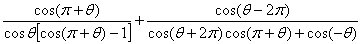 的值;
的值;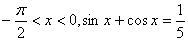 ,求
,求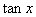 的值。
的值。 的终边过点
的终边过点 ,则
,则 的值为( )
的值为( )


 <α<0,则点P(tanα,cosα)位于 ( )
<α<0,则点P(tanα,cosα)位于 ( ) (2)
(2) 
 ,给出下列四个说法:
,给出下列四个说法: ,则
,则 ;②
;②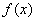 的最小正周期是
的最小正周期是 ;③
;③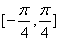 上是增函数; ④
上是增函数; ④ 对称. 其中正确说法的个数为( )
对称. 其中正确说法的个数为( )  为第二象限角,sin
为第二象限角,sin ,则cos
,则cos
