题目内容
设命题p: (x,y∈R),命题q:x2+y2≤r2(x、y、r∈R,r>0),若命题q是命题¬p的充分非必要条件,则r的最大值为
(x,y∈R),命题q:x2+y2≤r2(x、y、r∈R,r>0),若命题q是命题¬p的充分非必要条件,则r的最大值为
【答案】分析:此题是线性规划和解析几何中圆的知识相联系的一道综合题,解答时要充分利用好数形结合的思想对问题进行转化;同时针对与充要条件的信息可以得到:在q对应区域内的点一定在p对应的区域外部,在p对应区域外部的点一定不在q对应的区域内部.最终综合分析找到临界状态,列出求参数r的方程解出即可.
解答: 解:p所对应的区域为,
解:p所对应的区域为,
q对应的区域为以原点为圆心以r为半径的圆.
又在q对应区域内的点一定在p对应的区域外部,
在p对应区域外部的点一定不在q对应的区域内部.
所以当圆与直线3x+4y-12=0相切时,半径r最大,
此时r= .
.
故答案为:
点评:本题考查了线性规划问题、圆的知识还有充要条件问题,属综合类问题.针对于现行规划还有解析几何中的圆要善于利用数形结合,分析转化问题.针对于充要条件的知识要注意从两个角度分析推出还是推不出还有条件是什么、结论是什么.当然结合所有信息找出临界状态,从而找到一个方程解出一个参数的思维规律值得同学们反思整理.
解答:
 解:p所对应的区域为,
解:p所对应的区域为,q对应的区域为以原点为圆心以r为半径的圆.
又在q对应区域内的点一定在p对应的区域外部,
在p对应区域外部的点一定不在q对应的区域内部.
所以当圆与直线3x+4y-12=0相切时,半径r最大,
此时r=
 .
.故答案为:

点评:本题考查了线性规划问题、圆的知识还有充要条件问题,属综合类问题.针对于现行规划还有解析几何中的圆要善于利用数形结合,分析转化问题.针对于充要条件的知识要注意从两个角度分析推出还是推不出还有条件是什么、结论是什么.当然结合所有信息找出临界状态,从而找到一个方程解出一个参数的思维规律值得同学们反思整理.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
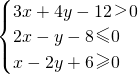 (x,y∈R),命题q:x2+y2≤r2(x、y、r∈R,r>0),若命题q是命题?p的充分非必要条件,则r的最大值为 ________
(x,y∈R),命题q:x2+y2≤r2(x、y、r∈R,r>0),若命题q是命题?p的充分非必要条件,则r的最大值为 ________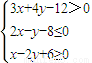 (x,y∈R),命题q:x2+y2≤r2(x、y、r∈R,r>0),若命题q是命题¬p的充分非必要条件,则r的最大值为
(x,y∈R),命题q:x2+y2≤r2(x、y、r∈R,r>0),若命题q是命题¬p的充分非必要条件,则r的最大值为 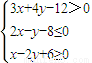 (x,y∈R),命题q:x2+y2≤r2(x,y,r∈R,r>0),若命题q是命题¬p的充分非必要条件,则r的取值范围是 .
(x,y∈R),命题q:x2+y2≤r2(x,y,r∈R,r>0),若命题q是命题¬p的充分非必要条件,则r的取值范围是 . (x,y,k∈R,且k>0)命题q:(x-3)2+y2≤25(x,y∈R),若P是q的充分不必要条件,则k的取值范围是( )
(x,y,k∈R,且k>0)命题q:(x-3)2+y2≤25(x,y∈R),若P是q的充分不必要条件,则k的取值范围是( )