题目内容
给出下列结论:
①当x≥2时,x+
的最小值是3;
②当0<x≤2时,2x+2-x存在最大值;
③若m∈(0,1],则函数y=m+
的最小值为2
;
④当x>1时,lgx+
≥2.
其中一定成立的结论序号是
①当x≥2时,x+
| 1 |
| x-1 |
②当0<x≤2时,2x+2-x存在最大值;
③若m∈(0,1],则函数y=m+
| 3 |
| m |
| 3 |
④当x>1时,lgx+
| 1 |
| lgx |
其中一定成立的结论序号是
①②④
①②④
(把成立的序号都填上).分析:变形利用基本不等式和利用导数研究函数的单调性即可得出.
解答:解:①当x≥2时,x+
=x-1+
+1≥2
+1=3,当且仅当x=2时取等号,∴x+
的最小值是3;
②令f(x)=2x+2-x,则f′(x)=2xln2-2-xln2=ln2(2x-
)≥0,∴函数f(x)单调递增,∴当x=2时,函数f(x)取得最大值4+
=
,因此正确.
③若m∈(0,1],∵y′=1-
=
<0,因此函数y=m+
单调递减,∴函数f(x)最小值为1+
=4,因此不正确;
④当x>1时,lgx0,∴lgx+
≥2
=2.当且仅当x=10时取等号.
综上可知:只有①②④正确.
故答案为①②④.
| 1 |
| x-1 |
| 1 |
| x-1 |
(x-1)•
|
| 1 |
| x-1 |
②令f(x)=2x+2-x,则f′(x)=2xln2-2-xln2=ln2(2x-
| 1 |
| 2x |
| 1 |
| 4 |
| 17 |
| 4 |
③若m∈(0,1],∵y′=1-
| 3 |
| m2 |
| m2-3 |
| m2 |
| 3 |
| m |
| 3 |
| 1 |
④当x>1时,lgx0,∴lgx+
| 1 |
| lgx |
lgx•
|
综上可知:只有①②④正确.
故答案为①②④.
点评:熟练掌握变形利用基本不等式和利用导数研究函数的单调性是解题的关键.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
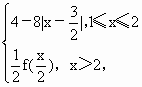 .给出下列结论:
.给出下列结论: