题目内容
若任取x1,x2∈[a,b],且x1≠x2,都有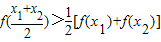 成立,则称f(x)是[a,b]上的凸函数,则下列函数中,是凸函数的为( )
成立,则称f(x)是[a,b]上的凸函数,则下列函数中,是凸函数的为( )A.y=sinx,
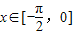
B.y=2-x2,x∈[0,2]
C.y=x2-x,x∈[-2,1]
D.y=x2,x∈[0,2]
【答案】分析:题中的代数式的几何意义是:函数在区间[a,b]上的图象是上凸的.因此根据这个几何意义,分别结合各个选项的相应区间上的图象加以判断,不难选出正确答案.
解答:解:f(x)是[a,b]上的凸函数,它的几何意义是
函数在区间[a,b]上的图象是上凸的
由此判断,y=sinx,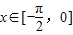 上的图象是下凹的,不符合题意,故A不正确;
上的图象是下凹的,不符合题意,故A不正确;
y=2-x2,x∈[0,2]上的图象是开口向下的抛物线,符合上凸,故B正确;
y=x2-x,x∈[-2,1]上的图象是开口向上的抛物线,不符合题意,故C不正确;
y=x2,x∈[0,2]上的图象是开口向上的抛物线,不符合题意,故D不正确;
故选B
点评:本题考查了函数的凹凸性及其几何意义,属于中档题.解题的关键是读懂题中的式子,将其转化为几何图象.
解答:解:f(x)是[a,b]上的凸函数,它的几何意义是
函数在区间[a,b]上的图象是上凸的
由此判断,y=sinx,
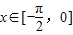 上的图象是下凹的,不符合题意,故A不正确;
上的图象是下凹的,不符合题意,故A不正确;y=2-x2,x∈[0,2]上的图象是开口向下的抛物线,符合上凸,故B正确;
y=x2-x,x∈[-2,1]上的图象是开口向上的抛物线,不符合题意,故C不正确;
y=x2,x∈[0,2]上的图象是开口向上的抛物线,不符合题意,故D不正确;
故选B
点评:本题考查了函数的凹凸性及其几何意义,属于中档题.解题的关键是读懂题中的式子,将其转化为几何图象.

练习册系列答案
相关题目
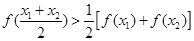 成立,则称f(x)
成立,则称f(x)
