题目内容
若任取x1,x2∈[a,b],且x1≠x2,都有f(
)<
[f(x1)+f(x2)]成立,则称f(x)是[a,b]上的凹函数.下列函数为凹函数的是( )
| x1+x2 |
| 2 |
| 1 |
| 2 |
分析:分别作出这几个函数的草图,再依据凹函数的概念,即可得到答案.
解答:解:作出函数f(x)=2x的图象,如右图
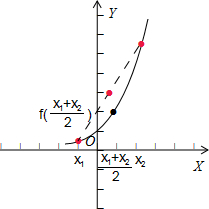 任取x1,x2∈[a,b],且x1≠x2,
任取x1,x2∈[a,b],且x1≠x2,
都有f(
)<
[f(x1)+f(x2)]成立,
故函数f(x)=2x即为凹函数.
故答案为 A
 任取x1,x2∈[a,b],且x1≠x2,
任取x1,x2∈[a,b],且x1≠x2,都有f(
| x1+x2 |
| 2 |
| 1 |
| 2 |
故函数f(x)=2x即为凹函数.
故答案为 A
点评:本题属于创新概念题,实际上是将高等数学的内容作为信息介绍给学生,考查考生的信息处理能力.这也是当今高考考题的一个趋势.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
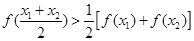 成立,则称f(x)
成立,则称f(x)
