题目内容
函数y=x3-2ax+a在（0，1）内有极小值的一个充分必要条件是分析：函数y=x3-2ax+a在（0，1）内有极小值的一个充分必要条件是其导函的数零点在区间（0，1）上，解出导函数的零点即可．
解答：解：∵y=x3-2ax+a
∴y′=3x2-2a，
令y′=0，得x=
，（负值舍去）
∵函数y=x3-2ax+a在（0，1）内有极小值，
∴0＜
＜1，
∴a∈（0，
）．
故填：（0，
）．
∴y′=3x2-2a，
令y′=0，得x=
|
∵函数y=x3-2ax+a在（0，1）内有极小值，
∴0＜
|
∴a∈（0，
| 3 |
| 2 |
故填：（0，
| 3 |
| 2 |
点评：本题主要考查利用导数研究函数的极值，借助于导数，将三次函数的单调性及极值（或最值）问题转化为二次函数进行研究．
练习册系列答案
超能学典应用题题卡系列答案
相关题目
函数y=x3-2ax+a在（0，1）内有极小值，则实数a的取值范围是（ ）
| A、（0，3） | ||
B、（0，
| ||
| C、（0，+∞） | ||
| D、（-∞，3） |
)
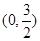C. 
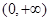D.
