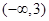题目内容
函数y=x3-2ax+a在(0,1)内有极小值,则实数a的取值范围是( )
| A、(0,3) | ||
B、(0,
| ||
| C、(0,+∞) | ||
| D、(-∞,3) |
分析:先对函数求导,函数在(0,1)内有极小值,得到导函数等于0时,求出x的值,这个值就是函数的极小值点,使得这个点在(0,1)上,求出a的值.
解答:解:根据题意,y'=3x2-2a=0有极小值则方程有解
a>0
x=±
所以x=
是极小值点
所以0<
<1
0<
<1
0<a<
故选B
a>0
x=±
|
所以x=
|
所以0<
|
0<
| 2a |
| 3 |
0<a<
| 3 |
| 2 |
故选B
点评:本题考查函数在某一点取得极值点条件,本题解题的关键是在一个区间上有极值相当于函数的导函数在这一个区间上有解.

练习册系列答案
相关题目
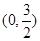 C.
C. 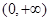 D.
D.