题目内容
若坐标原点在圆C:(x-m)2+(y+m)2=4的外部,则实数m的取值范围是
- A.(-1,1)
- B.
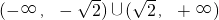
- C.

- D.
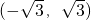
B
分析:若坐标原点在圆C:(x-m)2+(y+m)2=4的外部,则有原点到圆心的距离大于半径,由此求得实数m的取值范围.
解答:∵圆C:(x-m)2+(y+m)2=4,圆心坐标为(m,-m),半径等于2,
若坐标原点在圆C:(x-m)2+(y+m)2=4的外部,则有:(0-m)2+(0+m)2>4,
解得 m> 或 m<-
或 m<- ,故实数m的取值范围是
,故实数m的取值范围是 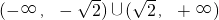 ,
,
故选B.
点评:本题主要考查点和圆的位置关系,两点间的距离公式以及一元二次不等式的解法,属于基础题.
分析:若坐标原点在圆C:(x-m)2+(y+m)2=4的外部,则有原点到圆心的距离大于半径,由此求得实数m的取值范围.
解答:∵圆C:(x-m)2+(y+m)2=4,圆心坐标为(m,-m),半径等于2,
若坐标原点在圆C:(x-m)2+(y+m)2=4的外部,则有:(0-m)2+(0+m)2>4,
解得 m>
 或 m<-
或 m<- ,故实数m的取值范围是
,故实数m的取值范围是 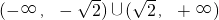 ,
,故选B.
点评:本题主要考查点和圆的位置关系,两点间的距离公式以及一元二次不等式的解法,属于基础题.

练习册系列答案
相关题目







