Question

(本小题12分) 命题p: 函数y=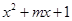在(-1, +)上单调递增, 命题函数y=lg[]的定义域为R.
(1)若“或”为真命题，求的取值范围;
(2)若“或”为真命题，“且”为假命题，求的取值范围.

Answer 1

(1) m>1; (2) 1<m<2或m3.

解析试题分析：命题P真则根据对称轴和定义域的关系得到a的范围。
命题q真则真数的值域包含所有的正实数?判别式大于0求出a的范围；
据p且q为假命题?命题p和q有且仅有一个为真．求出a的范围
解: p真: , 得m2;  q真: , 解得1<m<3.
(1) m>1; (2) p, q一真一假. 因此, 或, 解得: 1<m<2或m3.
考点：本题主要考查了命题的真值，以及二次不等式的恒成立问题，和二次函数的单调性的运用。
点评：解决该试题的关键是解决二次不等式恒成立问题常结合二次函数的图象列出需要满足的条件、复合命题的真假与构成其简单命题真假的关系．