ÌâÄ¿ÄÚÈÝ
ƽÃæÖ±½Ç×ø±êϵxOyÖУ¬ÒÑÖª¡ÑM¾¹ýµãF1£¨0£¬-c£©£¬F2£¨0£¬c£©£¬A£¨
c£¬0£©Èýµã£¬ÆäÖÐc£¾0£®
£¨1£©Çó¡ÑMµÄ±ê×¼·½³Ì£¨Óú¬cµÄʽ×Ó±íʾ£©£»
£¨2£©ÒÑÖªÍÖÔ²
+
=1(a£¾b£¾0)£¨ÆäÖÐa2-b2=c2£©µÄ×ó¡¢ÓÒ¶¥µã·Ö±ðΪD¡¢B£¬¡ÑMÓëxÖáµÄÁ½¸ö½»µã·Ö±ðΪA¡¢C£¬ÇÒAµãÔÚBµãÓҲ࣬CµãÔÚDµãÓҲ࣮
¢ÙÇóÍÖÔ²ÀëÐÄÂʵÄÈ¡Öµ·¶Î§£»
¢ÚÈôA¡¢B¡¢M¡¢O¡¢C¡¢D£¨OΪ×ø±êԵ㣩ÒÀ´Î¾ùÔÈ·Ö²¼ÔÚxÖáÉÏ£¬ÎÊÖ±ÏßMF1ÓëÖ±ÏßDF2µÄ½»µãÊÇ·ñÔÚÒ»Ìõ¶¨Ö±ÏßÉÏ£¿ÈôÊÇ£¬ÇëÇó³öÕâÌõ¶¨Ö±Ïߵķ½³Ì£»Èô²»ÊÇ£¬Çë˵Ã÷ÀíÓÉ£®
| 3 |
£¨1£©Çó¡ÑMµÄ±ê×¼·½³Ì£¨Óú¬cµÄʽ×Ó±íʾ£©£»
£¨2£©ÒÑÖªÍÖÔ²
| y2 |
| a2 |
| x2 |
| b2 |
¢ÙÇóÍÖÔ²ÀëÐÄÂʵÄÈ¡Öµ·¶Î§£»
¢ÚÈôA¡¢B¡¢M¡¢O¡¢C¡¢D£¨OΪ×ø±êԵ㣩ÒÀ´Î¾ùÔÈ·Ö²¼ÔÚxÖáÉÏ£¬ÎÊÖ±ÏßMF1ÓëÖ±ÏßDF2µÄ½»µãÊÇ·ñÔÚÒ»Ìõ¶¨Ö±ÏßÉÏ£¿ÈôÊÇ£¬ÇëÇó³öÕâÌõ¶¨Ö±Ïߵķ½³Ì£»Èô²»ÊÇ£¬Çë˵Ã÷ÀíÓÉ£®
£¨1£©Éè¡ÑMµÄ·½³ÌΪx2+y2+Dx+Ey+F=0£¬
ÔòÓÉÌâÉ裬µÃ
½âµÃ
¡ÑMµÄ·½³ÌΪx2+y2-
cx-c2=0£¬
¡ÑMµÄ±ê×¼·½³ÌΪ(x-
c)2+y2=
c2£»£¨5·Ö£©
£¨2£©¡ÑMÓëxÖáµÄÁ½¸ö½»µãA(
c£¬0)£¬C(-
c£¬0)£¬
ÓÖB£¨b£¬0£©£¬D£¨-b£¬0£©£¬
ÓÉÌâÉè
¼´
ËùÒÔ
½âµÃ
£¼
£¼
£¬
¼´
£¼e£¼
£®ËùÒÔÍÖÔ²ÀëÐÄÂʵÄÈ¡Öµ·¶Î§Îª(
£¬
)£»£¨10·Ö£©
£¨3£©ÓÉ£¨1£©£¬µÃM(
c£¬0)£®
ÓÉÌâÉ裬µÃ
c-b=b-
c=
c£®
¡àb=
c£¬D(-
c£¬0)£®
¡àÖ±ÏßMF1µÄ·½³ÌΪ
-
=1£¬
¢ÙÖ±ÏßDF2µÄ·½³ÌΪ-
+
=1£®
¢ÚÓÉ¢Ù¢Ú£¬µÃÖ±ÏßMF1ÓëÖ±ÏßDF2µÄ½»µãQ(
c£¬3c)£¬
Ò×ÖªkOQ=
Ϊ¶¨Öµ£¬
¡àÖ±ÏßMF1ÓëÖ±ÏßDF2µÄ½»µãQÔÚ¶¨Ö±Ïßy=
xÉÏ£®£¨15·Ö£©
ÔòÓÉÌâÉ裬µÃ
|
½âµÃ
|
¡ÑMµÄ·½³ÌΪx2+y2-
2
| ||
| 3 |
¡ÑMµÄ±ê×¼·½³ÌΪ(x-
| ||
| 3 |
| 4 |
| 3 |
£¨2£©¡ÑMÓëxÖáµÄÁ½¸ö½»µãA(
| 3 |
| ||
| 3 |
ÓÖB£¨b£¬0£©£¬D£¨-b£¬0£©£¬
ÓÉÌâÉè
|
|
ËùÒÔ
|
| 1 |
| 2 |
| c |
| a |
| ||
| 2 |
¼´
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
£¨3£©ÓÉ£¨1£©£¬µÃM(
| ||
| 3 |
ÓÉÌâÉ裬µÃ
| 3 |
| ||
| 3 |
| ||
| 3 |
¡àb=
2
| ||
| 3 |
2
| ||
| 3 |
¡àÖ±ÏßMF1µÄ·½³ÌΪ
| x | ||||
|
| y |
| c |
¢ÙÖ±ÏßDF2µÄ·½³ÌΪ-
| x | ||||
|
| y |
| c |
¢ÚÓÉ¢Ù¢Ú£¬µÃÖ±ÏßMF1ÓëÖ±ÏßDF2µÄ½»µãQ(
4
| ||
| 3 |
Ò×ÖªkOQ=
3
| ||
| 4 |
¡àÖ±ÏßMF1ÓëÖ±ÏßDF2µÄ½»µãQÔÚ¶¨Ö±Ïßy=
3
| ||
| 4 |

Á·Ï°²áϵÁдð°¸
 ÆÚÄ©1¾íËØÖʽÌÓýÆÀ¹À¾íϵÁдð°¸
ÆÚÄ©1¾íËØÖʽÌÓýÆÀ¹À¾íϵÁдð°¸
Ïà¹ØÌâÄ¿
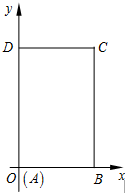 Èçͼ£¬ÔÚƽÃæÖ±½Ç×ø±êϵxOyÖУ¬ÒÑÖª¾ØÐÎABCDµÄÁ½±ßAB£¬CD·Ö±ðÂäÔÚxÖá¡¢yÖáµÄÕý°ëÖáÉÏ£¬ÇÒAB=2£¬AD=4£¬µãAÓë×ø±êÔµãÖغϣ®ÏÖ½«¾ØÐÎÕÛµþ£¬Ê¹µãAÂäÔÚÏ߶ÎDCÉÏ£¬ÈôÕÛºÛËùÔÚµÄÖ±ÏßµÄбÂÊΪk£¬ÊÔд³öÕÛºÛËùÔÚÖ±Ïߵķ½³Ì¼°kµÄ·¶Î§£®
Èçͼ£¬ÔÚƽÃæÖ±½Ç×ø±êϵxOyÖУ¬ÒÑÖª¾ØÐÎABCDµÄÁ½±ßAB£¬CD·Ö±ðÂäÔÚxÖá¡¢yÖáµÄÕý°ëÖáÉÏ£¬ÇÒAB=2£¬AD=4£¬µãAÓë×ø±êÔµãÖغϣ®ÏÖ½«¾ØÐÎÕÛµþ£¬Ê¹µãAÂäÔÚÏ߶ÎDCÉÏ£¬ÈôÕÛºÛËùÔÚµÄÖ±ÏßµÄбÂÊΪk£¬ÊÔд³öÕÛºÛËùÔÚÖ±Ïߵķ½³Ì¼°kµÄ·¶Î§£®