题目内容

设是抛物线的焦点，为抛物线上异于原点的两点，且满足．延长分别交抛物线于点（如图）．求四边形面积的最小值．

解析：设，由题设知，

直线的斜率存在，设为．

因直线过焦点，所以，直线

的方程为    ．

联立方程组，消得

由根与系数的关系知：，                 ……5分

于是

     　　　　  ……10分

又因为，所以直线的斜率为，

从而直线的方程为：，同理可得 ．……15分

故

当时等号成立．所以，四边形的最小面积为32．       ……20分

练习册系列答案
相关题目
已知抛物线y=ax2（a≠0）的准线方程为y=-1．
（Ⅰ）求抛物线的方程；
（Ⅱ）设F是抛物线的焦点，直线l：y=kx+b（k≠0）与抛物线交于A，B两点，记直线AF，BF的斜率之和为m．求常数m，使得对于任意的实数k（k≠0），直线l恒过定点，并求出该定点的坐标．
过曲线上一点与以此点为切点的切线垂直的直线，叫做曲线在该点的法线．
已知抛物线C的方程为y=ax2（a＞0，x≠0）．点M（x0，y0）是C上任意点，过点M作C的切线l，法线m．
（I）求法线m与抛物线C的另一个交点N的横坐标xN取值范围；
（II）设点F是抛物线的焦点，连接FM，过点M作平行于y轴的直线n，设m与x轴的交点为S，n与x轴的交点为K，设l与x轴的交点为T，求证∠SMK=∠FMN

（全国Ⅱ卷理15）已知是抛物线的焦点，过且斜率为1的直线交于两点．设，则与的比值等于        ．

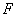 设是抛物线的焦点，过点M(－1，0)且斜率k=的直线顺次交抛物线于两点。

（Ⅰ）求实数m的取值范围。（Ⅱ）若与的夹角为，求抛物线的方程；

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网