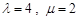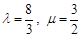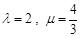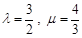题目内容
设x,y∈R,向量a=(x,1),b=(1,y),c=(2,-4),且a⊥c,b∥c,则|a+b|= ( ).
A.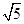 | B.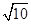 | C.2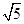 | D.10 |
B
∵a=(x,1),b=(1,y),c=(2,-4),
由a⊥c,得a·c=2x-4=0,∴x=2.
由b∥c,得1×(-4)-2y=0,∴y=-2.
因此a+b=(2,1)+(1,-2)=(3,-1),则|a+b|=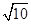 .
.
由a⊥c,得a·c=2x-4=0,∴x=2.
由b∥c,得1×(-4)-2y=0,∴y=-2.
因此a+b=(2,1)+(1,-2)=(3,-1),则|a+b|=
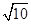 .
.
练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
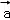 =(1,2),
=(1,2),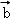 =(1,0),
=(1,0),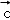 =(3,4).若λ为实数,(
=(3,4).若λ为实数,(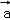 +λ
+λ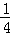

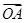 =(-3,1),
=(-3,1),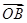 =(-2,k),则实数k=________.
=(-2,k),则实数k=________.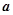 =(1,-3,2)平行的一个向量的坐标为( )
=(1,-3,2)平行的一个向量的坐标为( )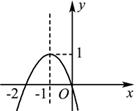
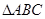 中,
中,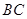 边上的中线AO长为2,若动点
边上的中线AO长为2,若动点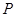 满足
满足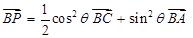
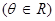 ,则
,则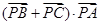 的最小值是 .
的最小值是 .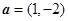 ,
,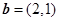 ,
,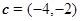 ,则下列结论中错误的是( )
,则下列结论中错误的是( )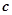 与向量
与向量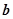 共线
共线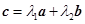 (
(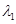 ,
,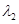
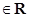 ),则
),则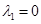 ,
,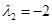
 ,都存在实数
,都存在实数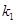 ,
,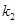 ,使得
,使得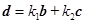
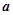 在向量
在向量
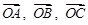 ,其中
,其中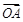 与
与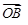 的夹角为
的夹角为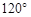 ,
,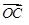 的夹角为
的夹角为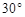 ,且
,且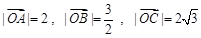 ,若
,若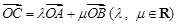 ,则( )
,则( )