题目内容
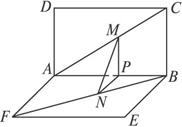
如图所示,正方形ABCD与正方形ABEF所在平面互相垂直,两个正方形边长均为2,M、N分别是AC和BF上的点,且AM=FN=x.(1)求证:MN∥平面BCE;
(2)设MN=y,求函数y=f(x);
(3)当MN最短时,求MN与AC、MN与FB所成的角.
思路解析:本题已知了面面垂直关系,容易想到利用面面垂直的性质,从而构造得到线面垂直关系.第一问要证明线面平行,紧紧围绕着线面平行的判定定理,去寻求相关的线线平行,充分利用正方形的性质,从而得到线线平行;第二问,在第一问的基础上,在相关的三角形中将MN表示出来,进而将第三个问题解决.
解:(1)作MP⊥AB于P,则有MP⊥平面ABFE.
连结PN,又BC⊥平面ABCD,
∴MP∥BC.∴![]() .
.
又AM=FN,AC=FB,
∴![]() .∴PN∥AF∥BE.
.∴PN∥AF∥BE.
故平面MPN∥平面BCE.MN![]() 平面MPN,∴MN∥平面BCE.
平面MPN,∴MN∥平面BCE.

(2)∵AM=x,MP=AP=![]() x,
x,
又PN=PB=![]() ,
,
从而由MP⊥平面ABFE知MP⊥PN,MN=![]() .
.
∴y= (3)由(2)得y= ∴MN∥EC. ∴MN与AC所成的角是∠ACE(或其补角). 易知△ACE为正三角形,故MN与AC所成的角是60°. 同理,MN与FB所成的角是60°.![]() (0
(0![]() .当x=1时,MN有最小值为1,此时M、N分别为两个正方形的中心,∴
.当x=1时,MN有最小值为1,此时M、N分别为两个正方形的中心,∴![]() .
.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
 如图所示,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,CD=2AB=2AD.
如图所示,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,CD=2AB=2AD. 如图所示,直线AB的方程为6x-3y-4=0,向边长为2的正方形内随机地投飞镖,飞镖都能投入正方形内,且投到每个点的可能性相等,则飞镖落在阴影部分(三角形ABC的内部)的概率是( )
如图所示,直线AB的方程为6x-3y-4=0,向边长为2的正方形内随机地投飞镖,飞镖都能投入正方形内,且投到每个点的可能性相等,则飞镖落在阴影部分(三角形ABC的内部)的概率是( ) (2012•金华模拟)如图所示的正方形中,将边AB、AD各4等分,分别作AB、AD的平行线段成4×4方格网,则从图中取出一由网格线形成的矩形,恰好为正方形的概率是
(2012•金华模拟)如图所示的正方形中,将边AB、AD各4等分,分别作AB、AD的平行线段成4×4方格网,则从图中取出一由网格线形成的矩形,恰好为正方形的概率是 如图所示,正方形AA1D1D与矩形ABCD所在平面互相垂直,AB=2AD=2,点E为AB的中点.
如图所示,正方形AA1D1D与矩形ABCD所在平面互相垂直,AB=2AD=2,点E为AB的中点.