题目内容
实系数方程x2+ax+2b=0的一个根大于0且小于1,另一个根大于1且小于2,则![]() 的取值范围是
的取值范围是
[ ]
A.(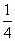 ,1)
,1)
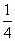 ,1)
,1)B.(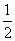 ,1)
,1)
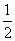 ,1)
,1)C.(-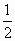 ,
,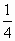 )
)
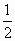 ,
,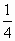 )
)D.(-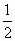 ,
,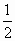 )
)
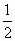 ,
,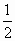 )
)
答案:A
解析:
解析:
|
|

练习册系列答案
相关题目
题目内容
实系数方程x2+ax+2b=0的一个根大于0且小于1,另一个根大于1且小于2,则![]() 的取值范围是
的取值范围是
[ ]
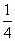 ,1)
,1)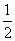 ,1)
,1)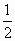 ,
,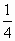 )
)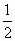 ,
,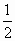 )
)|
|
