题目内容
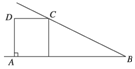
如图,一直角梯形ABCD,AB⊥AD,AD⊥DC,AB=2, ,CD=1,E为AD中点,沿CE,BE把梯形折成四个面都是直角三角形的三棱锥,使A,D重合,则三棱锥的体积等于( )
,CD=1,E为AD中点,沿CE,BE把梯形折成四个面都是直角三角形的三棱锥,使A,D重合,则三棱锥的体积等于( )
A.

B.

C.

D.

【答案】分析:由平面图象中的垂直关系找到几何体中的线面垂直关系,再分别求底面积和高即可求体积
解答:解:在直角梯形ABCD中,过点C作CF⊥AB,则四边形AFCD是正方形,则在直角三角形BCF中BF=1,BC= ,则CF=AD=
,则CF=AD= ,则AE=
,则AE=
∵四边形ABCD是直角梯形,AB⊥AD,AD⊥DC
∴在三棱锥E-ABC中,AE⊥AC,AE⊥AB
又∵AC∩AB=A,且AC?面ABC,AB?面ABC
∴AE⊥面ABC
又底面△ABC中AC=1,AB=2,BC= ,满足AC2+BC2=AB2
,满足AC2+BC2=AB2
则底面△ABC是直角三角形
∴底面△ABC的面积为S=
∴三棱锥的体积为V=
故选C
点评:本题考查几何体的体积,同时考查了线面垂直的证明.求几何体的体积,常用的方法有直接法、割补法、等积转化法等.在翻折问题中要注意有些长度和垂直平行关系是不改变的,需注意条件的灵活应用.属简单题
解答:解:在直角梯形ABCD中,过点C作CF⊥AB,则四边形AFCD是正方形,则在直角三角形BCF中BF=1,BC=
 ,则CF=AD=
,则CF=AD= ,则AE=
,则AE=
∵四边形ABCD是直角梯形,AB⊥AD,AD⊥DC
∴在三棱锥E-ABC中,AE⊥AC,AE⊥AB
又∵AC∩AB=A,且AC?面ABC,AB?面ABC
∴AE⊥面ABC
又底面△ABC中AC=1,AB=2,BC=
 ,满足AC2+BC2=AB2
,满足AC2+BC2=AB2 则底面△ABC是直角三角形
∴底面△ABC的面积为S=

∴三棱锥的体积为V=

故选C
点评:本题考查几何体的体积,同时考查了线面垂直的证明.求几何体的体积,常用的方法有直接法、割补法、等积转化法等.在翻折问题中要注意有些长度和垂直平行关系是不改变的,需注意条件的灵活应用.属简单题

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
 如图,一直角梯形ABCD,AB⊥AD,AD⊥DC,AB=2,
如图,一直角梯形ABCD,AB⊥AD,AD⊥DC,AB=2,