题目内容
如图，一直角梯形ABCD的上、下底分别为CD＝
，AB＝3，高AD＝2，求以腰BC所在直线为轴旋转一周所形成的旋转体的表面积．
解析] 由题设∠ABC＝30°，BC＝4，分别过A、D作AM⊥BC，DN⊥BC垂足为M，N，
则AM＝
，DN＝
，所求旋转体的表面积由三部分构成
①圆锥B－AM的侧面积S1＝π·AM·AB＝
.
②圆台MN的侧面积S2＝π(AM＋DN)·AD＝4π.
③圆锥C－DN的侧面积S3＝π·DN·CD＝
π.
∴S表＝S1＋S2＋S3＝(15＋4)π.
练习册系列答案
相关题目
如图，一直角梯形ABCD，AB⊥AD，AD⊥DC，AB=2，
，AB＝3
，AB＝3
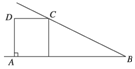
，CD=1，E为AD中点，沿CE，BE把梯形折成四个面都是直角三角形的三棱锥，使A，D重合，则三棱锥的体积等于（ ）
