题目内容
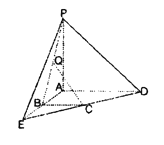
【题目】如图，在五面体
中，四边形
是矩形，
，
，
，
，
为
的中点，
为线段
上一点，且
.
（Ⅰ）求证：
平面
；
（Ⅱ）求证：
；
（Ⅲ）求证：平面
平面
.
【答案】(Ⅰ)证明见解析；(Ⅱ)证明见解析；(Ⅲ)证明见解析.
【解析】
试题分析：
(1)连接
交
于
点，则为的中点，连接
.由三角形中位线的性质可得
.结合线面平行的判定定理可得
平面
.
(2)连接
.由几何关系可证得四边形
是平行四边形.则
，结合直角三角形的性质和题意可得
，则
.
(3)由题意可知
为等边三角形，则
.同理可得
.利用线面垂直的判定定理可得
平面
，结合面面垂直的判定定理可得平面
平面
.
试题解析：
（Ⅰ）连接交于点，则为的中点，连接.
∵在
中，为的中点，
为
的中点.
∴.
∵
平面，
平面，
∴平面.
（Ⅱ）连接.
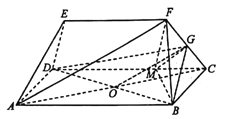
∵四边形
是矩形，
，
∴
，且
.
∵
，
，
，
∴
.
∵
，
，
∴
.
∴四边形是平行四边形.
∴，
.
∵在
中，
，
，，
∴
.
∵在
中，，
，
，
∴是直角三角形.
∴.
∴.
（Ⅲ）∵在中，
，
∴为等边三角形.
∵为的中点，
∴.
同理，由
为等边三角形，可得.
∵
，
∴平面.
∵
平面，
∴平面平面.
开心快乐假期作业暑假作业西安出版社系列答案【题目】某快餐代卖店代售多种类型的快餐，深受广大消费者喜爱.其中，
种类型的快餐每份进价为
元，并以每份
元的价格销售.如果当天20:00之前卖不完，剩余的该种快餐每份以
元的价格作特价处理，且全部售完.
（1）若该代卖店每天定制
份种类型快餐，求种类型快餐当天的利润
（单位：元）关于当天需求量
（单位：份，
）的函数解析式；
（2）该代卖店记录了一个月
天的种类型快餐日需求量（每天20:00之前销售数量）
日需求量 |
|
|
|
|
|
|
天数 |
|
|
|
|
|
|
（i）假设代卖店在这一个月内每天定制份种类型快餐，求这一个月种类型快餐的日利润（单位：元）的平均数（精确到
）；
（ii）若代卖店每天定制份种类型快餐，以天记录的日需求量的频率作为日需求量发生的概率，求种类型快餐当天的利润不少于
元的概率.
