题目内容
函数y=ax-2+2(a>0,a≠1)的图象恒过定点A,若定点A在直线ax+by-6=0上,其中a•b>0,则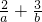 的最小值为
的最小值为
- A.

- B.

- C.

- D.4
A
分析:定点A的坐标为(2,3),代入直线ax+by-6=0 可得 得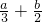 =1,故有
=1,故有 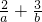 =(
=( 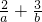 )×(
)×(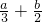 ),使用基本不等式求得其最小值.
),使用基本不等式求得其最小值.
解答:函数y=ax-2+2(a>0,a≠1)的图象恒过定点A的坐标为(2,3),代入直线ax+by-6=0 可得
2a+3b=6,∴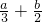 =1,则
=1,则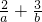 =(
=( 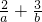 )×(
)×(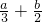 )=
)= +
+ +
+ +
+ ≥
≥ +2=
+2= ,
,
当且仅当 a=b时,取等号,
故选 A.
点评:本题考查基本不等式的应用,函数的图象过定点问题,得到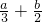 =1,
=1,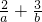 =(
=( 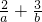 )×(
)×(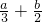 ),是解题的关键.
),是解题的关键.
分析:定点A的坐标为(2,3),代入直线ax+by-6=0 可得 得
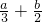 =1,故有
=1,故有 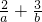 =(
=( 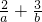 )×(
)×(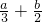 ),使用基本不等式求得其最小值.
),使用基本不等式求得其最小值.解答:函数y=ax-2+2(a>0,a≠1)的图象恒过定点A的坐标为(2,3),代入直线ax+by-6=0 可得
2a+3b=6,∴
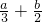 =1,则
=1,则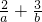 =(
=( 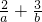 )×(
)×(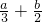 )=
)= +
+ +
+ +
+ ≥
≥ +2=
+2= ,
,当且仅当 a=b时,取等号,
故选 A.
点评:本题考查基本不等式的应用,函数的图象过定点问题,得到
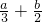 =1,
=1,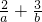 =(
=( 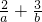 )×(
)×(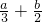 ),是解题的关键.
),是解题的关键. 
练习册系列答案
相关题目