Question

（2013•朝阳区一模）函数f（x）是定义在R上的偶函数，且满足f（x+2）=f（x）．当x∈[0，1]时，f（x）=2x．若在区间[-2，2]上方程ax+a-f（x）=0恰有三个不相等的实数根，则实数a的取值范围是

[0，1）

．

Answer 1

分析：在区间[-2，2]上，函数f（x）与y=a（x+1）的图象有三个不同的交点，由函数的性质可作出它们的图象，由斜率公式可得边界，进而可得答案．

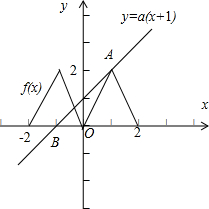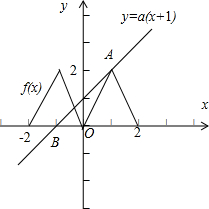解答：解：在区间[-2，2]上方程ax+a-f（x）=0恰有三个不相等的实数根，等价于在区间[-2，2]上，函数f（x）与y=a（x+1）的图象有三个不同的交点，
由f（x+2）=f（x）可得函数的周期为2，且为偶函数，如图所示：
由于直线y=a（x+1）过定点B（-1，0），当直线的斜率a=0时，满足条件，当直线过点A（1，2）时，a=1，不满足条件．
数形结合可得实数a的取值范围是[0，1），
故答案为[0，1）．

点评：本题考查方程根的存在性及个数的判断，数形结合是解决问题的关键，属于中档题．