题目内容
已知等差数列{an}中,a10=5,a13=20,求a50.
思路解析:通过a10=5和a13=20先求出a1和d,再利用通项公式求a50是基本方法. 解法一:设数列{an}的首项为a1,公差为d,则 解得 ∴a50=a1+49d=-40+49×5=205. 解法二:∵a13=a10+3d, ∴d= 所以a50=a10+40d=5+40×5=205. 解法三:令an=pn+q, 则 ∴an=5n-45. 所以a50=5×50-45=205. 深化升华 解法二中a13=a10+3d,可以解释为a10是“新”数列的首项,则a13就是该“新”数列的第4项(非第3项);解法三中an=pn+q是等差数列通项公式的变形式,利用该式解等差数列问题,也是常用方法之一.
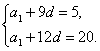
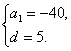
![]() =5.
=5.![]() 解得
解得![]()
 练习册系列答案
练习册系列答案
百渡期末综合测试系列答案
聊城中考系列答案
学业测评一卷通小学升学试题汇编系列答案
小学单元综合练习与检测系列答案
实验探究报告练习册系列答案
单元学习体验与评价系列答案
黄冈小状元小学升学考试冲刺复习卷系列答案
毕业总复习冲刺卷系列答案
学习指导系列答案
随堂同步练习系列答案
相关题目
 , 则
, 则
 的值是
的值是  B.
B.
 C.
C.
 D.
D.
