题目内容
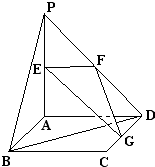 (2008•温州模拟)如图,平面PAD⊥平面ABCD,ABCD为正方形,∠PAD=90°,且PA=AD=2,E、F、G分别是线段PA、PD、CD的中点.
(2008•温州模拟)如图,平面PAD⊥平面ABCD,ABCD为正方形,∠PAD=90°,且PA=AD=2,E、F、G分别是线段PA、PD、CD的中点.(1)求证:PB∥平面EFG;
(2)求异面直线EG与BD所成的角;
(3)在线段CD上是否存在一点Q,使得点A到平面EFQ的距离为
| 4 | 5 |
分析:(1)取AB中点H,连接GH,HE,易知E,F,G,H四点共面,根据中位线定理可知EH∥PB,又EH?面EFG,PB?平面EFG,满足线面平行的判定定理所需条件;
(2)取BC的中点M,连接GM、AM、EM,则GM∥BD,∠EGM(或其补角)就是异面直线EG与BD所成的角,在Rt△MGE中,利用余弦定理求出此角即可;
(3)假设在线段CD上存在一点Q满足题设条件,过点Q作QR⊥AB于R,连接RE,过A作AT⊥ER于T,可知AT就是点A到平面EFQ的距离,设CQ=x(0≤x≤2),在Rt△EAR中利用等面积法可求出x,从而求出所求.
(2)取BC的中点M,连接GM、AM、EM,则GM∥BD,∠EGM(或其补角)就是异面直线EG与BD所成的角,在Rt△MGE中,利用余弦定理求出此角即可;
(3)假设在线段CD上存在一点Q满足题设条件,过点Q作QR⊥AB于R,连接RE,过A作AT⊥ER于T,可知AT就是点A到平面EFQ的距离,设CQ=x(0≤x≤2),在Rt△EAR中利用等面积法可求出x,从而求出所求.
解答:解:(1)证明:取AB中点H,连接GH,HE,
∵E,F,G分别是线段PA、PD、CD的中点,
∴GH∥AD∥EF,
∴E,F,G,H四点共面.…(1分)
又H为AB中点,
∴EH∥PB.…(2分)
又EH?面EFG,PB?平面EFG,
∴PB∥面EFG.…(3分)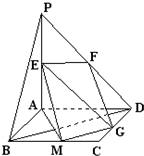
(2)解:取BC的中点M,连接GM、AM、EM,则GM∥BD,
∴∠EGM(或其补角)就是异面直线EG与BD所成的角.…(4分)
在Rt△MAE中,EM=
=
,
同理EG=
,又GM=
BD=
,
∴在Rt△MGE中,cos∠EGM=
=
…(7分)
故异面直线EG与BD所成的角为arccos
.…(8分)
(3)假设在线段CD上存在一点Q满足题设条件.
过点Q作QR⊥AB于R,连接RE,则QR∥AD.
∵ABCD是正方形,△PAD是直角三角形,且PA=AD=2,
∴AD⊥AB,AD⊥PA,
又AB∩PA=A,
∴AD⊥平面PAB.
又∵E,F分别是PA,PD中点,
∴EF∥AD,∴EF⊥平面PAB
又EF?面EFQ,
∴面EFQ⊥平面PAB.
过A作AT⊥ER于T,则AT⊥面EFQ,
∴AT就是点A到平面EFQ的距离.…(12分)
设CQ=x(0≤x≤2),则BR=CQ=x,AR=2-x,AE=1,
在Rt△EAR中,AT=
=
=
解得x=
.
故存在点Q,当CQ=
时,点A到平面EFQ的距离为
…(14分)
∵E,F,G分别是线段PA、PD、CD的中点,
∴GH∥AD∥EF,
∴E,F,G,H四点共面.…(1分)
又H为AB中点,
∴EH∥PB.…(2分)
又EH?面EFG,PB?平面EFG,
∴PB∥面EFG.…(3分)

(2)解:取BC的中点M,连接GM、AM、EM,则GM∥BD,
∴∠EGM(或其补角)就是异面直线EG与BD所成的角.…(4分)
在Rt△MAE中,EM=
| EA2+AM2 |
| 6 |
同理EG=
| 6 |
| 1 |
| 2 |
| 2 |
∴在Rt△MGE中,cos∠EGM=
| EG2+GM2-ME2 |
| 2EG•GM |
| ||
| 6 |
故异面直线EG与BD所成的角为arccos
| ||
| 6 |
(3)假设在线段CD上存在一点Q满足题设条件.

过点Q作QR⊥AB于R,连接RE,则QR∥AD.
∵ABCD是正方形,△PAD是直角三角形,且PA=AD=2,
∴AD⊥AB,AD⊥PA,
又AB∩PA=A,
∴AD⊥平面PAB.
又∵E,F分别是PA,PD中点,
∴EF∥AD,∴EF⊥平面PAB
又EF?面EFQ,
∴面EFQ⊥平面PAB.
过A作AT⊥ER于T,则AT⊥面EFQ,
∴AT就是点A到平面EFQ的距离.…(12分)
设CQ=x(0≤x≤2),则BR=CQ=x,AR=2-x,AE=1,
在Rt△EAR中,AT=
| AR•AE |
| RE |
| (2-x)•1 | ||
|
| 4 |
| 5 |
解得x=
| 2 |
| 3 |
故存在点Q,当CQ=
| 2 |
| 3 |
| 4 |
| 5 |
点评:本题主要考查了线面平行的判定,以及异面直线所成角和点到面的距离的度量,同时考查了空间想象能力和推理论证能力,属于中档题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目