题目内容
在锐角三角形中,边a、b是方程x2-2 x+2=0的两根,角A、B满足2sin(A+B)-
x+2=0的两根,角A、B满足2sin(A+B)- =0,求角C的度数,边c的长度.
=0,求角C的度数,边c的长度.
【答案】
C=60°,c=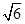 。
。
【解析】
试题分析:由2sin(A+B)-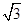 =0,得sin(A+B)=
=0,得sin(A+B)= 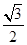 ,
,
∵△ABC为锐角三角形, ∴A+B=120°, C=60°,
又∵a、b是方程x2-2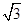 x+2=0的两根,
x+2=0的两根,
∴a+b=2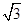 ,
a·b=2, ∴c2=a2+b2-2a·bcosC=(a+b)2-3ab=12-6=6, ∴c=
,
a·b=2, ∴c2=a2+b2-2a·bcosC=(a+b)2-3ab=12-6=6, ∴c=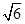 。
。
考点:本题主要考查余弦定理、两角和与差的三角函数。
点评:本题具有一定综合性,三角形和一元二次方程相结合,运用余弦定理解题。

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案
相关题目
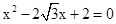 的两根,
的两根, ,求角C的度数,边c的长度及三角形ABO的面积
,求角C的度数,边c的长度及三角形ABO的面积