题目内容
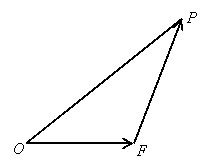 如图,设△
如图,设△ 的面积为
的面积为 ,已知
,已知 .
.
(1)若 ,求向量
,求向量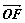 与
与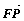 的夹角
的夹角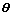 的取值范围;
的取值范围;
(2)若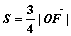 ,且
,且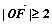 ,当
,当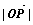 取最小值时,建立适当的直角坐标系,求以
取最小值时,建立适当的直角坐标系,求以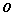 为中心,
为中心,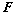 为一个焦点且经过点
为一个焦点且经过点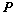 的椭圆方程.
的椭圆方程.
【答案】
(1)由题意知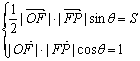 , 可得
, 可得 .--------2分
.--------2分
∵ ,
∴
,
∴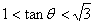 , 有
, 有 . --------6分
. --------6分
(2)以 为原点,
为原点, 所在直线为
所在直线为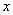 轴建立直角坐标系,
轴建立直角坐标系,
设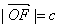 ,点
,点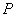 的坐标为
的坐标为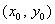 ,
,
∵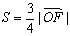 , ∴
, ∴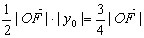 ,
, 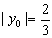 .
.
∴ , ∴
, ∴ . ------8分
. ------8分
设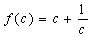 ,则当
,则当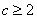 时,有
时,有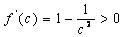 .
.
∴ 在
在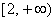 上增函数,∴当
上增函数,∴当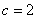 时,
时, 取得最小值
取得最小值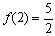 ,
,
从而 取得最小,此时
取得最小,此时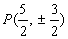 . ---------------------11分
. ---------------------11分
设椭圆方程为 ,
,
则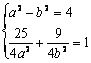 ,解之得
,解之得 ,故
,故 .--------12分
.--------12分

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
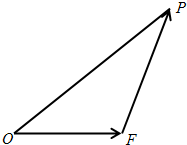 如图,设△OEP的面积为S,已知
如图,设△OEP的面积为S,已知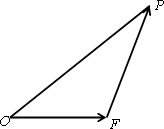
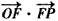 =1,
=1,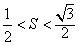 ,求向量
,求向量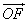 与
与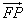 的夹角θ的取值范围;
的夹角θ的取值范围;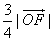 且
且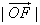 ≥2,当
≥2,当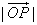 取最小值时,建立适当的直角坐标系,求以O为中心,F为一个焦点且经过点P的椭圆方程。
取最小值时,建立适当的直角坐标系,求以O为中心,F为一个焦点且经过点P的椭圆方程。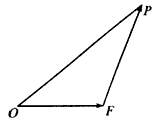
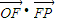 =1.
=1.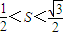 ,求向量
,求向量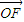 与
与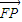 的夹角θ的取值范围;
的夹角θ的取值范围; |
|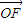 |,且|
|,且|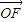 |≥2,当|
|≥2,当|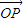 |取最小值时,建立适当的直角坐标系,求以O为中心,F为一个焦点且经过点P的椭圆方程.
|取最小值时,建立适当的直角坐标系,求以O为中心,F为一个焦点且经过点P的椭圆方程.
 =1.
=1. ,求向量
,求向量 与
与 的夹角θ的取值范围;
的夹角θ的取值范围; |
| |,且|
|,且| |≥2,当|
|≥2,当| |取最小值时,建立适当的直角坐标系,求以O为中心,F为一个焦点且经过点P的椭圆方程.
|取最小值时,建立适当的直角坐标系,求以O为中心,F为一个焦点且经过点P的椭圆方程.